: 정수를 2진수로 표현하는 방식에서 음수에 대해서는 어떻게 표현하냐에 대한 내용
음수를 나타내는 방식에는 3가지의 방식이 있다.
1. Signed Magnitude representation
➡️ 최상위 bit를 부호 bit로 생각해서 최상위 bit가 0이면 양수, 1이면 음수로 결정하는 것
2. Signed 1's Complement representation
➡️ 1의 보수를 음수로 결정하는 것
3. Signed 2's Complement representation
➡️ 2의 보수를 음수로 결정하는 것
이제 실제로 3 bit에서 위의 각각의 방식으로 음수를 나타내보자.
Signed Magnitude representation
0 1 1 ➡️ + 3
0 1 0 ➡️ + 2
0 0 1 ➡️ + 1
0 0 0 ➡️ + 0
1 0 0 ➡️ - 0
1 0 1 ➡️ - 1
1 1 0 ➡️ - 2
1 1 1 ➡️ - 3
Signed 1's Complement representation
0 1 1 ➡️ + 3
0 1 0 ➡️ + 2
0 0 1 ➡️ + 1
0 0 0 ➡️ + 0
0 0 0의 1의 보수 = 1 1 1 ➡️ - 0
0 0 1의 1의 보수 = 1 1 0 ➡️ - 1
0 1 0의 1의 보수 = 1 0 1 ➡️ - 2
0 1 1의 1의 보수 = 1 0 0 ➡️ - 3
Signed 2's Complement representation
0 1 1 ➡️ + 3
0 1 0 ➡️ + 2
0 0 1 ➡️ + 1
0 0 0 ➡️ + 0
0 0 0의 2의 보수 = 0 0 0이라, +0과 같아서 굳이 작성하지 않음.
0 0 1의 2의 보수 = 1 1 1 ➡️ - 1
0 1 0의 2의 보수 = 1 1 0 ➡️ - 2
0 1 1의 2의 보수 = 1 0 1 ➡️ - 3
1 0 0 ➡️ - 4

2의 보수로 음수를 만드는 방식은 0이 겹치지 않기 때문에 서로 다른 8개의 값을나타낼 수 있어서 나머지 방식보다 훨씬 효율적이다.
4bit 에서 음수 표현을 해보면 아래와 같다.
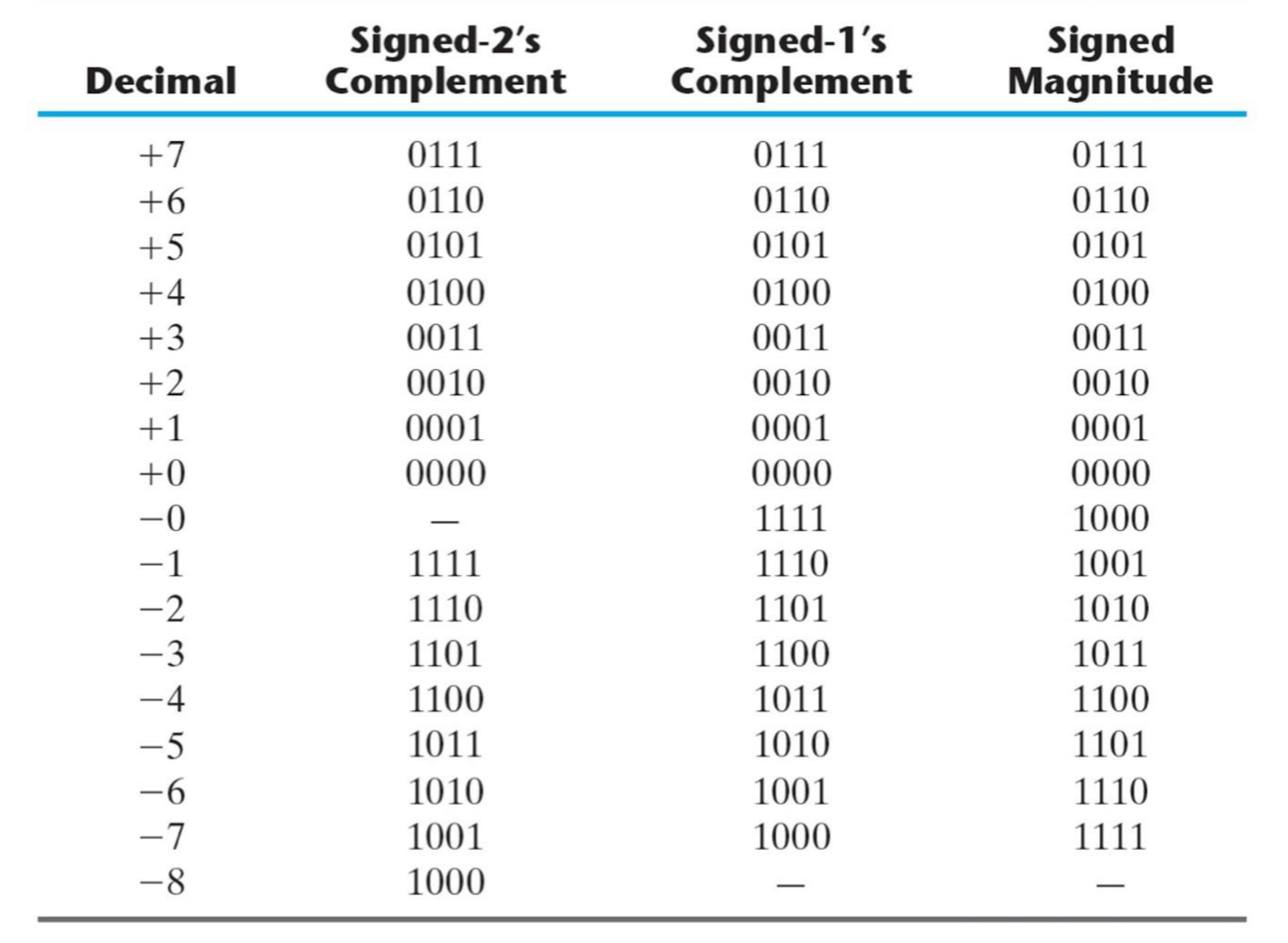

Signed 2's Complement representation로 10진수를 표현할 때 max와 min
3bit
max: 0 1 1 ➡️ 3
min: 1 0 0 ➡️ -4
따라서, 3bit에서는 -4 ~ 0 ~ 3을 표현할 수 있다.
4bit
max: 0 1 1 1 ➡️ 7
min: 1 0 0 0 ➡️ -8
따라서, 4bit에서는 -8 ~ 0 ~ 7을 표현할 수 있다.
8bit
max: 0 1 1 1 1 1 1 1 ➡️ 2의 7승 - 1
min: 1 0 0 0 0 0 0 0 ➡️ - 2의 7승
따라서, 4bit에서는 - 2의 7승 ~ 0 ~ (2의 7승 -1) 을 표현할 수 있다.
따라서 일반화하면 아래와 같다.
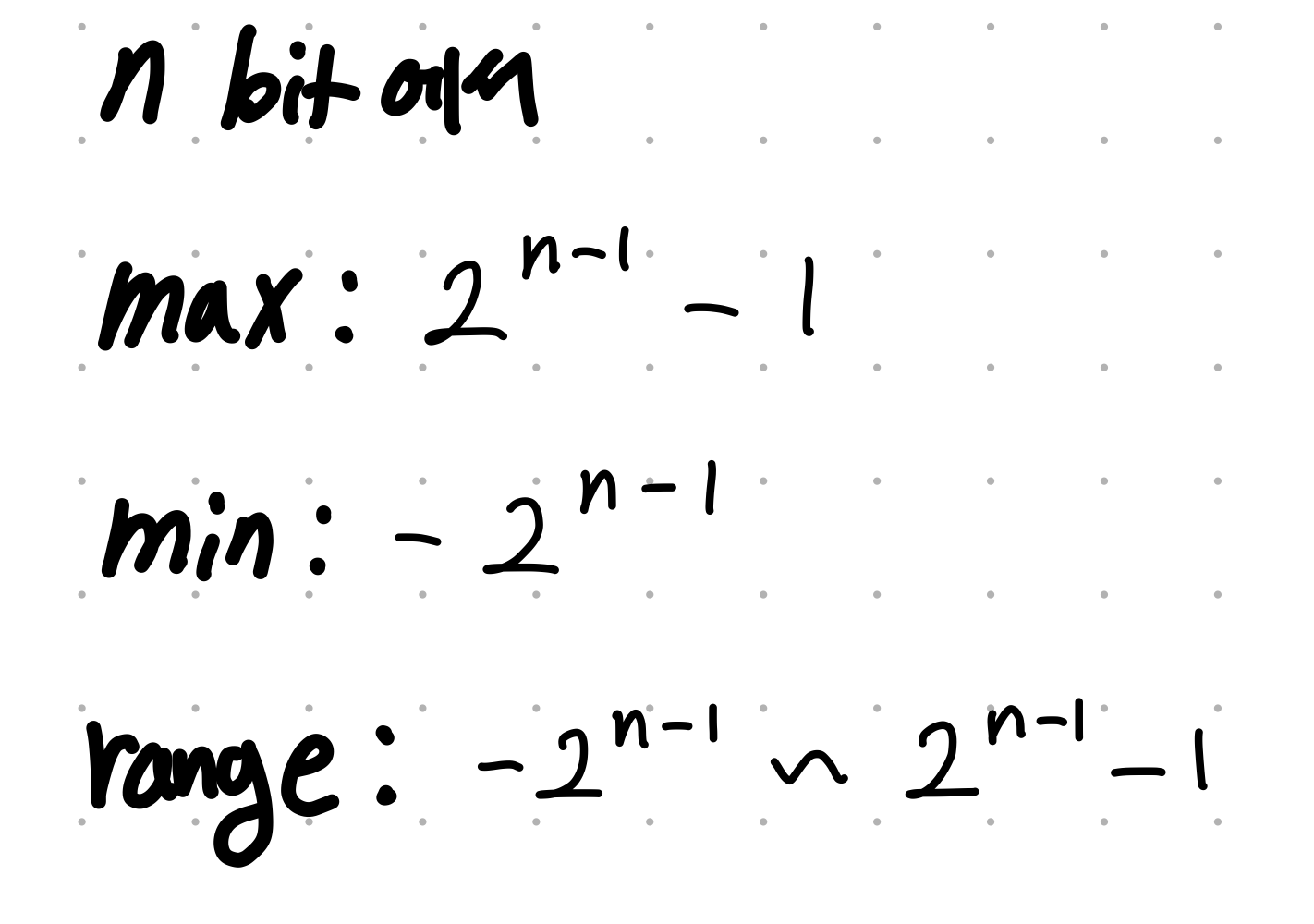
따라서 이런 범위를 넘어가는 값을 답으로 요구하는 연산에서는 범위를 넘어가는 오류. 즉, Over flow가 발생한다.
Over flow
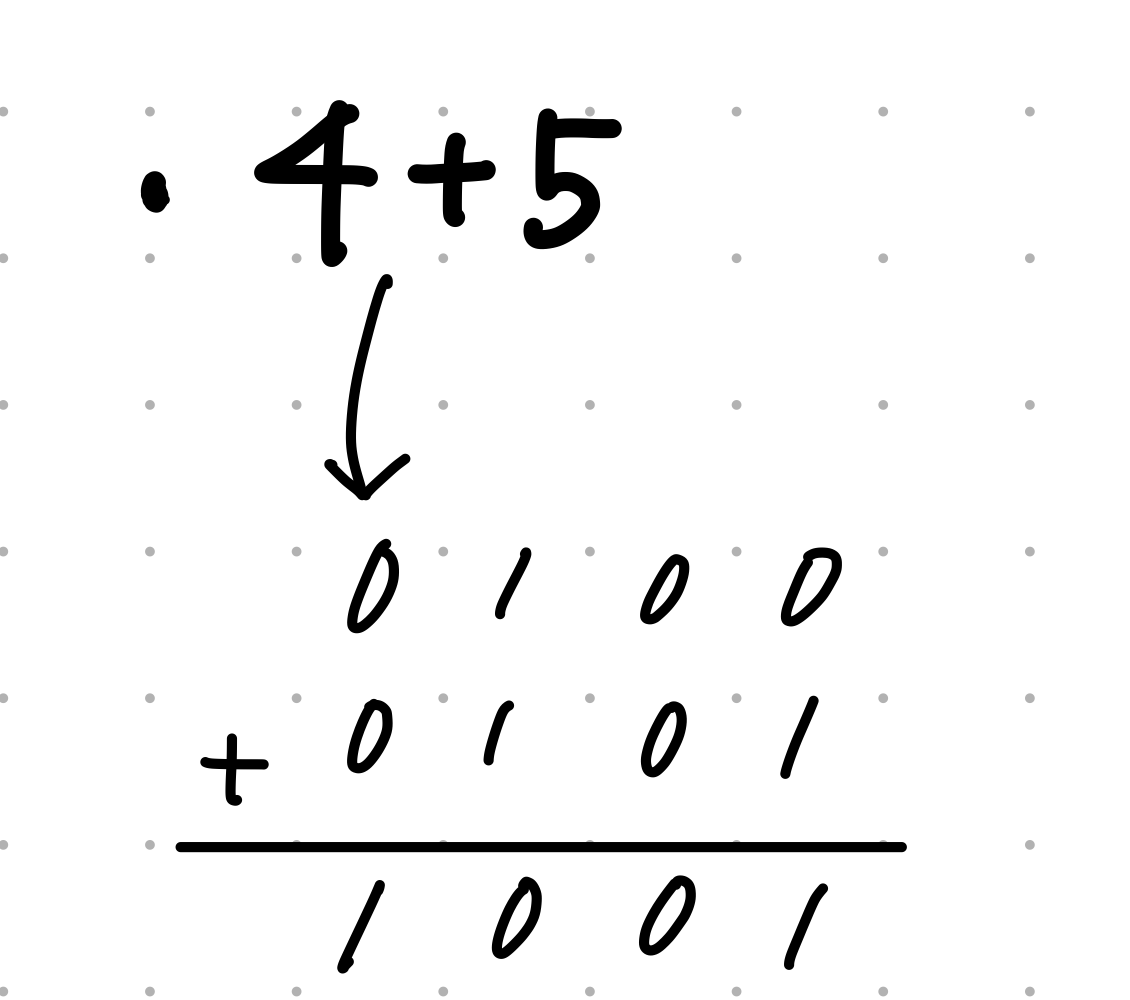
따라서 이와 같이 3bit가 표현할 수 있는 최대 값인 7을 넘는 9를 답으로 가져오는 연산에서는 Over flow가 발생한다.
계산해보면 최상위 bit가 1이기 때문에 음수를 표현하기 때문에 최상위 bit (-1) * 8 + 나머지 bit 0 * 4 + 0 * 2 + 1 * 1이므로 답은 -7이 나오게된다.
Over flow인 결과를 파악하는 방법
end carry = 최상위 bit의 carry ➡️ Over Flow 발생!!!
end carry ≠ 최상위 bit의 carry ➡️ Over Flow 발생 x

'2학년 2학기 > 컴퓨터 구조' 카테고리의 다른 글
| 3.5 Other binary codes (1) | 2024.10.06 |
|---|---|
| 3.4 Floating point representation(부동 소수점 표현) (1) | 2024.10.06 |
| 3.2 Complements(보수) (1) | 2024.10.06 |
| 3.1 Data types (1) | 2024.10.06 |
| 2024.10.02 - ch2관련 문제 (0) | 2024.10.02 |



