Training NN part(1)
1. CNN 전이학습

위처럼 대형 Data Set에서 CNN을 이용해서 Feature map을 추출하고 Feature map을 기반으로 Classifier를 통해서 분류를 했을 때 1000개 Class가 나온다고 가정하자.
하지만 우리가 실제로 필요한 10개라고 했을 때 1000개의 클래스가 아닌 10개의 클래스가 필요하다. 그랬을 때는 모든 학습을 다시 하는 것이 아니라 뒤에 있는 Classifier만 다시 학습해서 대형 Data Set을 통해서 나온 Feature map은 유지하되, Classifier만 다시 학습시킨다.
이게 바로 CNN 전이 학습이다.
2. 활성화 함수를 사용하는 이유
CNN이나 다른 신경망에서 선형적인 연산(곱셈, 덧셈)만으로는 복잡한(비선형)패턴이나 특징을 학습하는데 한계가 있다.
이 때, 활성화 함수를 이용하면 비선형적인 특징을 학습할 수 있게 된다. 활성화 함수는 각 뉴런의 출력 값을 비선형적으로 반환해서, 네트워크가 복잡하고 비선형적인 데이터 간의 관계를 학습할 수 있도록 도와준다.

예를 들어 우리는 이미지에서 귀, 입과 같은 비선형적인 특징을 추출하고 싶다. 하지만 CNN만으로는 비선형적 특징을 추출하는데 한계가 있다. 따라서, 활성화 함수를 이용해서 비성형적인 특징을 추출할 수 있다.
3. 활성화 함수 Sigmoid 함수에서 포화 문제가 생기는 원리는?

0또는 1에 가까워지면 기울기가 소실이 되는데, 기울기가 소실이 되면 학습을 하지 않게된다. 따라서 0또는 1에 뭉치는 포화현상이 일어난다.
3-1. "빠른 수렴 = 빠른 학습 속도" 인가?
아래에서 수렴이란 결과에 도달하는 것이라고 했다.
따라서 빠른 학습 속도이기 때문에 결과에 빨리 도달하는 것이라고 생각할 수 있다.
3-2. 수렴이란?
수렴이란, 결과에 도달하는 것이다.
예를 들어 모델이 고양이와 강아지를 판단하는 모델이 있다면 처음에는 강아지 이미지를 줘도 결과 Score로 0.4만 가져오던 모델이 점점 학습되면서 Score 0.9를 가져오게 되는 것이 바로 수렴이라고 한다.
3-3 .활성화 함수에서 X축(입력)이 가지는 의미는?
X축은 이미지의 데이터가 바로 들어오는 것이 아니라, Layer 거쳐서 나오는 출력값이 다시 활성화 함수에 들어갈 때 생기는 입력 값이다. 따라서 음수가 나올 수도, 양수가 나올 수 있다.
일반적으로, 양수로 나오는 값은 의미가 있다고 판단하고 음수가 나오는 값은 의미가 없다고 판단해서 활용을 하지 않는다.
3-4. 활성화 함수에서 기울기가 가지는 의미는?
기울기의 절대값이 크면 많이 업데이트하고, 기울기의 접대값이 작으면 조금 업데이트 시킨다.
4. Leaky ReLU와 ELU의 차이점


음수와 같은 노이즈가 있는 데이터가 입력으로 들어가게 되는 경우 Leaky ReLU는 끝도 없이 음수로 향하지만, ELU는 특정 지점에서 멈추게 된다.
따라서 노이즈가 있는 데이터가 입력 값을 들어올 경우 Leaky ReLU는 계속 학습에 영향을 끼치지만, ELU는 특정 지점에 도달하면 학습에 영향을 끼치지 않게 되어 노이즈에 강한 저항성을 가지게 된다.
5. normalized data - 이미지에서 많이 사용하는 과정
이미지에서는 0~255 사이의 큰 범위를 가지는데, 이처럼 값의 차이가 큰 경우 모델 학습에 영향을 미칠 수 있다.
예를 들어 이미지의 필셀 값중 255는 매우 큰 값이므로, 이런 값은 모델의 Gradient에 큰 영향을 미칠 수 있다. 반면에 작은 값들은 상대적으로 영향을 덜 미치게 된다. 이러한 차이는 학습의 편차를 만들어 특정 데이터가 지나치게 중요해지거나, 무시되는 현상이 생기게 된다.
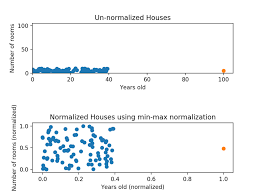
normalized data는 이러한 문제를 해결하기 위해서 모든 데이터를 0과 1사이 또는 -1과 1사이로 변환하여 이 값들의 크기를 일정하게 조정해준다.
이렇게 되면 아래와 같은 좋은 점이 생긴다.
1. 모든 값이 비슷한 범위에 있으므로 특정 값이 과도한 영향을 주지 않게 된다.
2. Gradient 계산시 데이터 간의 차이가 줄어, 모델이 안정적으로 학습이 가능하다.
3. 표준편차가 1로 조정되면서 데이터 간의 편차가 줄어들어, 학습속도 상승과 성능 상승 효과를 기대할 수 있다.
6. PCA
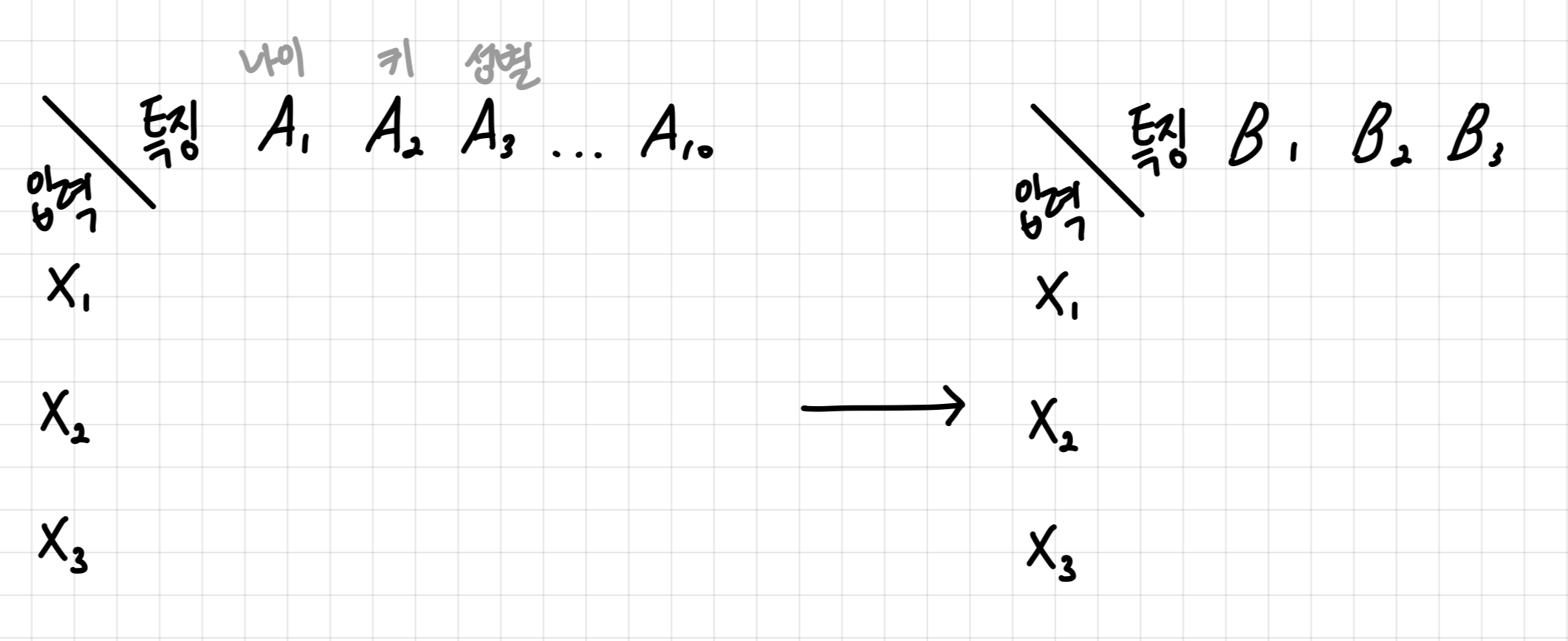
한마디로 말하자면, 예를 들어 10개의 특징들이 있다면 그 10개의 특징들을 서로 연관되는 것 끼리 묶어 특징을 압축시키는 것이다. 이때 압축 된 특징들은 서로 독립적이어야한다.
독립적(겹치는 것이 없는 것)이어햐 하는 이유는 최대한 많은 정보를 담기 위해서이다.
만약에 서로 겹치는 정보를 많이 가진다면, 불필요하게 중복된 정보가 생기고 표현할 수 있는 정보의 다양성이 줄어든다.
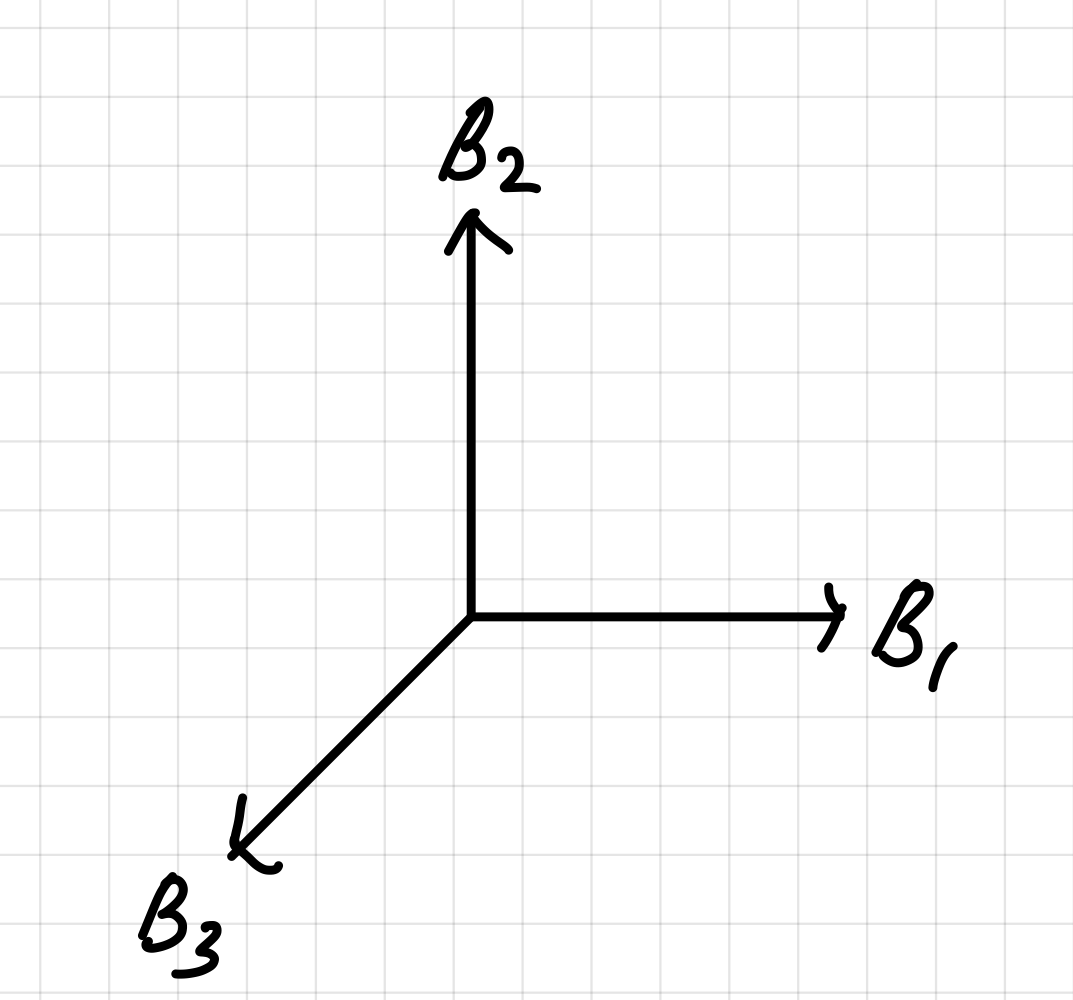
따라서, 이렇게 겹치지 않는 정보를 가진 특징 축으로 만드는 것이 PCA이다.
특징을 압축하는 방식
1. A1 ~ A10 중에서 가장 공통된 특징을 찾아서 B1으로 만든다.
2. B1과 겹치지 않는 특징을 가지면서 그 다음으로 A1 ~ A10 중에서 가장 공통된 특징을 찾아서 B2로 만든다.
3. B1, B2와 겹치지 않는 특징을 가지면서 그 다음으로 A1 ~ A10 중에서 가장 공통된 특징을 찾아서 B3로 만든다.
이렇게 특징을 줄이면 좋은 점은 가중치가 줄어들기 때문에 연산해야할 규모가 작아지고 학습이 더 빠르고 쉽게 진행될 수 있다.
7. 가중치가 0으로 초기화될 경우 왜 동일하게 학습될까?
가중치가 0일 때 모델 예측 값이 3이고 실제 정답 값은 4라고 가정하면 두 값의 Loss는 1이다. 이 Loss를 기반으로 역전파를하면 다 같은 가중치 0을 갖고 있기 때문에 서로 같은 가중치로 업데이트되고 또 반복되어 같은 가중치를 업데이트 하게된다.
따라서 뉴런 간의 가중치 차이가 생기지 않아 학습의 의미가 사라진다.
의미 있는 학습을 만들기 위해서는 모든 뉴런이 동일하지 않은 값으로 초기화 되어야한다.
8. 작은 난수로 가중치를 초기화 했을 때, 깊은 네트워크에서 가중치가 0이 되는 이유는?
가중치가 0.01일 때 Layer를 지나면서 0.001, 0.000001처럼 점점 0에 가까워지기 때문에 나중에는 0이 된다.
9. Xavier, He Initialization의 차이는 무엇인지?
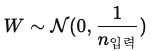
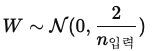
우선 해당 수식은 0이 평균이고 1/n 또는 2/n이 분산이다.
즉, He Initialization은 Xavier Initialization보다 분모가 크기 때문에 분산이 크다.
분산이 크다는 것은 그만큼 많이 퍼져있다는 의미이므로 음수에서도 많은 뉴런이 죽지만 양수에서는 더 많은 뉴런이 활성화될 수 있다.
따라서 He가 ReLU에서 학습이 유리한 이유는 ReLU는 양수의 범위가 클수록 학습에 유리하기 때문에 He가 ReLU에 적합하다!
10. Batch Normalization
: 신경망의 각 레이어에서 나오는 값을 평균이 0이고 분산이 1인 상태로 변환해서 학습을 안정화하고 속도를 높이는 방법이다.
따라서, 아래의 사진과 같이 데이터를 0을 기준으로 분포되게하고 분산을 1로 만들어 데이터가 일정한 범위 내에서 분포하도록 하는 것이다.
이렇게하면 데이터들 간의 편차가 줄어들어 하나의 데이터에 편향되는 문제를 해결할 수 있다. 결론적으로 기울기의 소실이나 기울기 폭주 같은 문제를 방지하면서 학습을 더욱 안정적으로 진행할 수 있다.
11. 0이 중심이 아니라는 것은 왜 학습에 불리한가?
출력 값이 항상 양수가 나오면 Gradient를 구할 때 항상 기울기 양수라서 가중치가 너무 크니깐 가중치를 줄여라! 라는 결과만 도출되게 된다. 결국 가중치는 늘지 않고 계속 감소하는 형태가 나온다.
하지만 0이 중심이 되면, 양수와 음수 모두 나올 수 있기 때문에 기울기가 양수면 가중치를 줄이고, 기울기가 음수면 가중치를 증가시켜라! 라는 결과가 도출되어 양방향으로 가중치가 업데이트 된다.
Training NN part(2)
1. Learning rate(학습률)이란?
신경망 학습 과정에서 가중치를 얼마나 빠르게 업데이트할지 결정하는 값이다.
2. Learning rate(학습률)이 클 때와 작을 때와 장점과 단점

즉, 학습률이 클때는 빠르게 결과까지 도달할 수는 있지만 정확한 값에 도달하기는 어렵다.
하지만 학습률이 작으면 결과까지 도달하는 시간이 느리지만 정확한 값에 도달하기 쉽다.
따라서, 두 방식을 혼합해서 시간에 따라 초반에는 학습률을 크게 만들어 결과까지 빠르게 도달하게 만들고, 후반에는 학습률을 줄여 정확한 결과값에 근접하기 쉽게 만드는 것이 가장 좋은 방식이다.
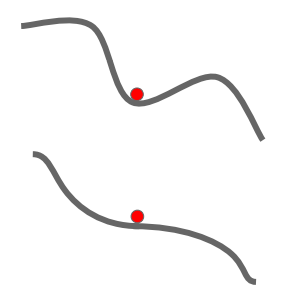
3. 모멘텀이란? (시각적)
모멘텀이랑 관성이다.
아래의 사진을 보면 위쪽 - 모멘텀(관성)이 없다면 회색 경로에게 상승해! 라고 하면, 많이 상승하고 하강해! 라고 하면 많이 하강하는 모습을 볼 수있다. 하지만 아래쪽 - 모멘텀(관성)이 있다면 회색 경로에게 상승해! 라고 하면, 나는 원래 위치를 유지하고 싶은데? 라고 하면서 조금만 상승하고 하강하는 모습을 볼 수 있다.
4. AdaGrad Update의 자주 등장하는 가중치는 Learning rate(학습률)가 낮아지고, 자주 등장하지 않는 가중치는 Learning rate(학습률) 높아져 효율적인 학습이 가능해진다는 이야기는 무슨 의미인가?
가중치가 자주 등장한다는 이야기는 기울기 제곱의 합이 커진다는 이야기이다. 기울기 제곱의 합. 즉, 분모가 커지면 그 값은 작아지므로 가중치는 작게 업데이트 되고, 가중치가 작게 업데이트 되면 학습률이 그만큼 낮아진다.
아래의 사진을보면 가중치가 자주 등장해 기울기의 제곱합이 64가 되어 가중치는 10에서 9.95로 0.05줄었다. 하지만 자주 등장하지 않는 가중치는 기울기의 제곱합이 16이 되어 가중치는 10에서 9.9로 1이 줄었다.

5. AdaGrad의 어떤 단점으로 RMSProp Update가 나왔고, 어떻게 해결 했는지?
단점은 지속적인 학습을 하게되면 가중치가의 제곱이 누적되고, 누적될 수록 가중치 업데이트의 폭은 줄어들어서 더이상 가중치가 업데이트되지 않고 학습률이 떨어지게 된다는 것이다.
따라서 이런 문제를 해결하고자 RMSProp이 나오게 되었다. 이 방식은 기울기 제곱의 누적 합이 아니라, 기울기 제곱의 평균을 구해서 분모가 계속 커지지 않도록 해결했다.
즉, Sum에서 Average로 변경했다.
6. Dropout
Dropout은 학습 시 일부 뉴런을 0으로 만들고 나머지 뉴런만 학습 시키고, 테스트 단계에서 모든 뉴런을 사용해서 테스트를 진행해 특정 뉴런이 특정 특징만 학습할 수 없도록 만드는 과정이다.
예를 들어 20%의 뉴런을 0으로 만들고 80%의 뉴런만 학습을 진행하고 테스트 단계에서 모든 뉴런을 사용한다면 기존 출력값에서 20%가 추가된다.
이러한 추가되는 출력을 해결하기 위해서 Dropout 학습시 사용되었던 뉴런의 퍼센트를 출력에 곱해주어 나온 값을 진짜 출력값으로 본다.
예를 들어 출력값이 1.212가 나왔다면 1.212 x 0.8 = 0.969를 출력 값으로 사용하게 된다.
CNN
1. CNN
CNN은 Feature mapd을 추출하는 단계인 Convoulution Layer까지를 CNN이라고 한다.
2. Fully Connected Layer
Fully Connected Layer란, Neural Network와 같은 형태라고 생각하면 된다.
즉, Neural Network를 생각해보면, 입력이 들어왔을 때 그 입력을 기반으로 분류작업을 하듯이 Fully Connected Layer 또한, 입력으로 Feature map이 들어오면, 해당 객체가 어떤 클래스에 속하는지 판단한다.
그리고 한 가지 기능이 더 있는데, 바로 출력 수를 조절할 수 있다.
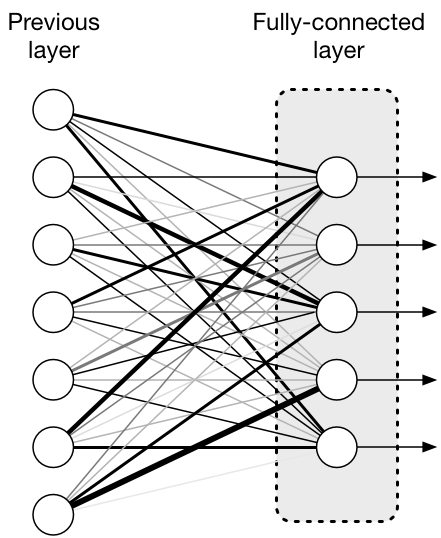
즉, 100개의 입력 이 들어왔다고 가정했을 때, Fully Connected Layer의 노드의 개수를 10개로 설정하면 100개의 입력에 각각 가중치를 곱하고 그 값들을 모두 합산한 것이 출력으로 나가게된다.
예를 들어 1번 노드는 1~100까지의 입력과 가중치를 곱하고 모두 합산한 값을 출력으로 보내고 2번도 마찬가지 ... 10번까지 출력 값으로 보내 10개의 출력 값이 생긴다.
3. ResNet
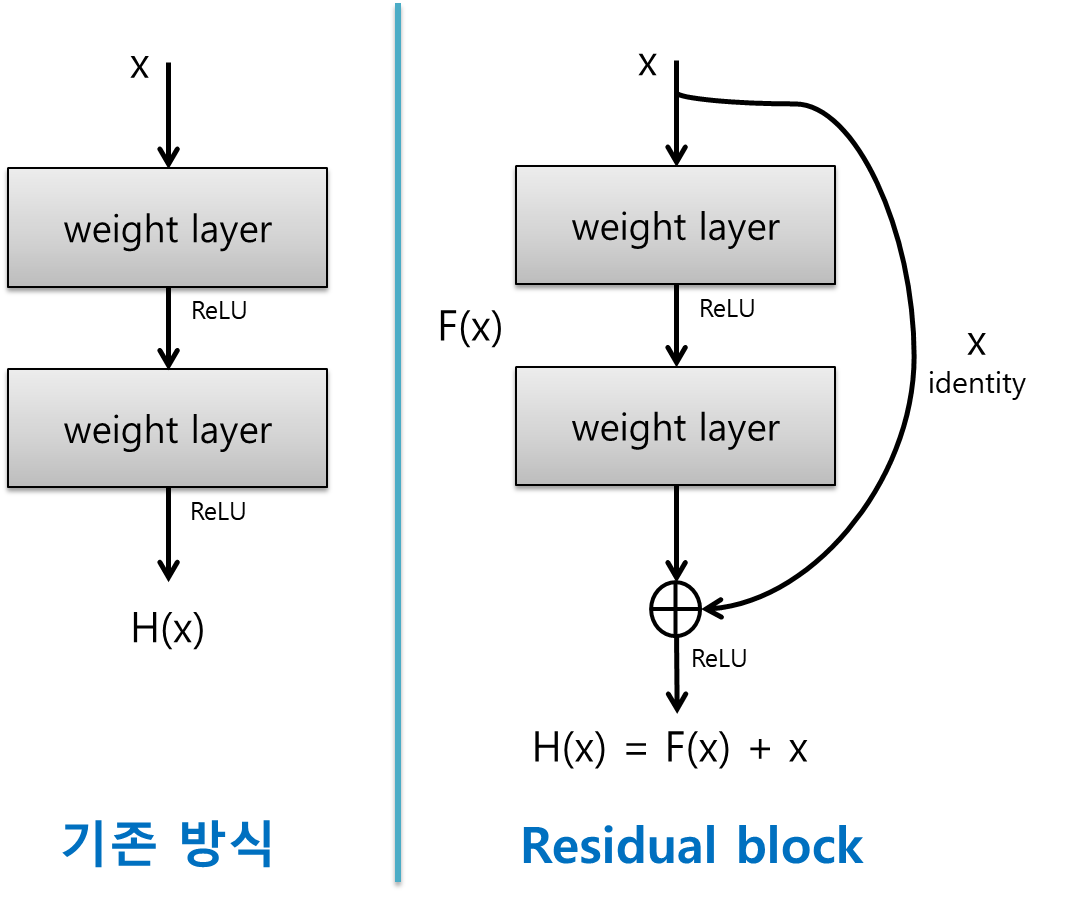
기존의 방식의 문제는 깊은 Layer로 갈수록 입력 데이터의 크기는 점점 줄어드는 문제가 생긴다.
하지만 ResNet은 데이터의 크기가 줄어들지 않는다. 레이어를 통해서 나온 값에 원본 데이터를 더해주고 또 다음 레이어를 통해서 나온 값에 원본 데이터를 더해주기 때문에 입력 데이터의 중요한 정보가 사라지지 않고, 데이터의 크기도 보존된다.
데이터를 더해주면 유지되는게 아니라 늘어나느거 아닌가? 라고 생각할 수 있지만, 더한 다는 건 행렬 덧셈이라고 생각하면된다.
아래의 사진과 같이 데이터는 늘어나는게 아니다.

따라서 원본의 데이터 x를 유지한 채로 변환된 값을 더해줌으로써, 데이터의 중요한 특징을 잃지 않고, 네트워크가 깊어지더라도 기울기 소실 문제를 해결할 수 있다.
Localization and Detection
1. 회귀와 분류의 차이?
회귀(Regression):
- 회귀는 연속적인 값을 예측하는 문제입니다. 즉, 예측 값이 실수 범위의 값으로, 특정한 간격이 없습니다. 예를 들어, 집의 가격을 예측하거나 온도를 예측할 때 사용됩니다.
- 회귀의 결과는 연속적인 수치로 나옵니다. 예를 들어, 어떤 모델이 0.1, 0.2, 0.3과 같은 값을 예측하면, 이는 각각 연속적인 수치를 의미하고, 특정 범주(기린, 코끼리, 말 등)에 속하지 않습니다. 모델이 예측한 값은 단순히 수치적 차이를 의미하는 것이며, 이 값들을 통해 구체적인 실수를 예측하는 것이 목표입니다.
예시:
- 집 값 예측에서 모델이 200,000달러나 300,000달러 같은 연속적인 값을 예측합니다. 이 값 사이에는 무수히 많은 다른 값들이 존재할 수 있습니다.
분류(Classification):
- 분류는 이산적인 클래스(즉, 카테고리)를 예측하는 문제입니다. 결과 값은 특정 범주에 속하는지를 결정하는 것이 목표입니다. 예를 들어, 고양이냐 강아지냐를 구분하는 문제에서는 모델이 각각의 입력 데이터에 대해 특정 범주(고양이, 강아지)로 분류합니다.
- 분류 문제에서는 출력이 클래스 레이블로 나옵니다. 이 경우 출력은 특정 범주에 해당하며, 그 중간 값은 특정 클래스에 대한 확률로 해석될 수 있습니다.
예시:
- 고양이와 강아지 분류에서 모델이 0을 출력하면 강아지, 1을 출력하면 고양이라고 한다면, 0.1이나 0.8 같은 값이 나올 때는 확률적 해석이 가능합니다. 예를 들어, 0.1이면 강아지일 확률이 90%, 고양이일 확률이 10%일 수 있습니다. 출력값이 연속적이어도 이 값은 클래스 레이블 사이의 확률로 해석되는 것이지, 실수 자체를 예측하는 것은 아닙니다.
즉, 회귀는 값에 의미를 두고 분류는 값이 의미하는 클래스에 의미를 두는 것이다!
2. Localization의 학습과정(Classification Head, Regression Head)
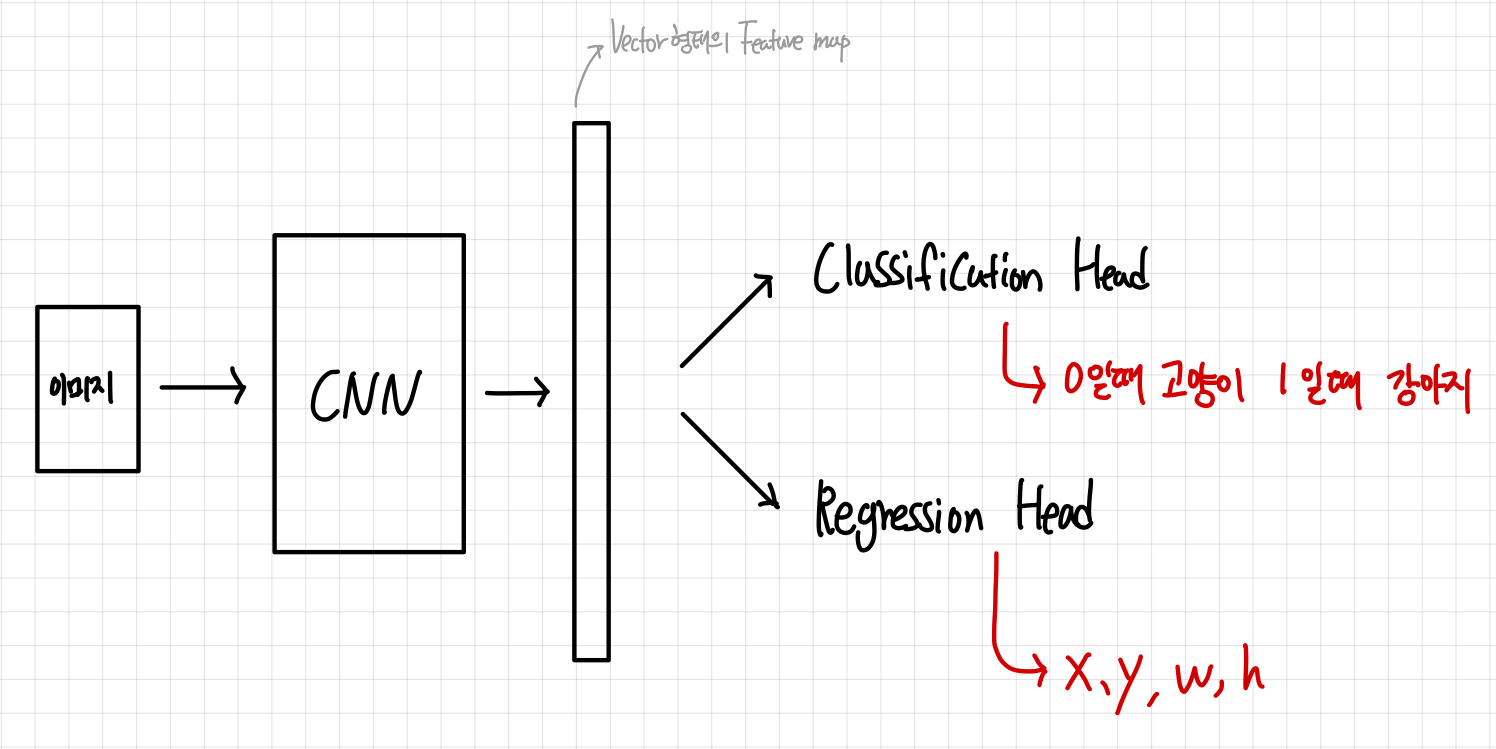
x, y, w, h의 값은 어떻게 나오게 되는건가?
x, y, w, h에 대한 실제 Label이 존재하고, 예측한 값과 실제 Label의 Loss를 구하고 또 반복하면서 점점 Loss를 줄이도록 학습하게 만들어 결국 x, y, w, h의 값이 나오게된다.
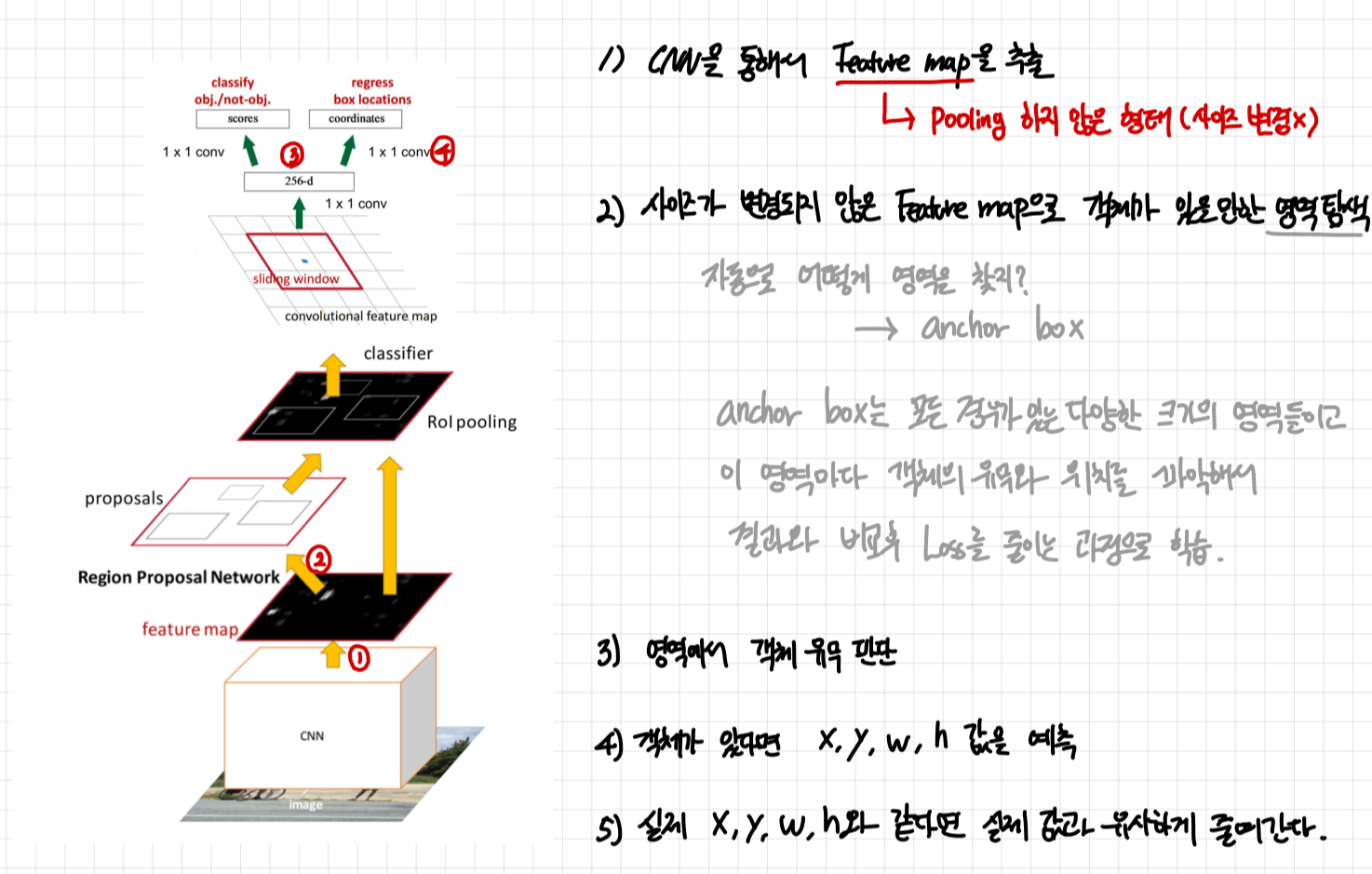
3. RPN
'CVLab > cs231n (2016)' 카테고리의 다른 글
| cs231n - lecture10(RNN) (1) | 2024.10.09 |
|---|---|
| cs231n - lecture09(CNN의 시각화 및 이해) (5) | 2024.10.06 |
| cs231n - lecture08(Localization and Detection) (1) | 2024.10.03 |
| cs231n - lecture07(CNN) (0) | 2024.10.01 |
| cs231n - lecture06(Trainit NN Part 2) (0) | 2024.09.28 |



