NN 구조에 대한 굉장히 쉬운 설명
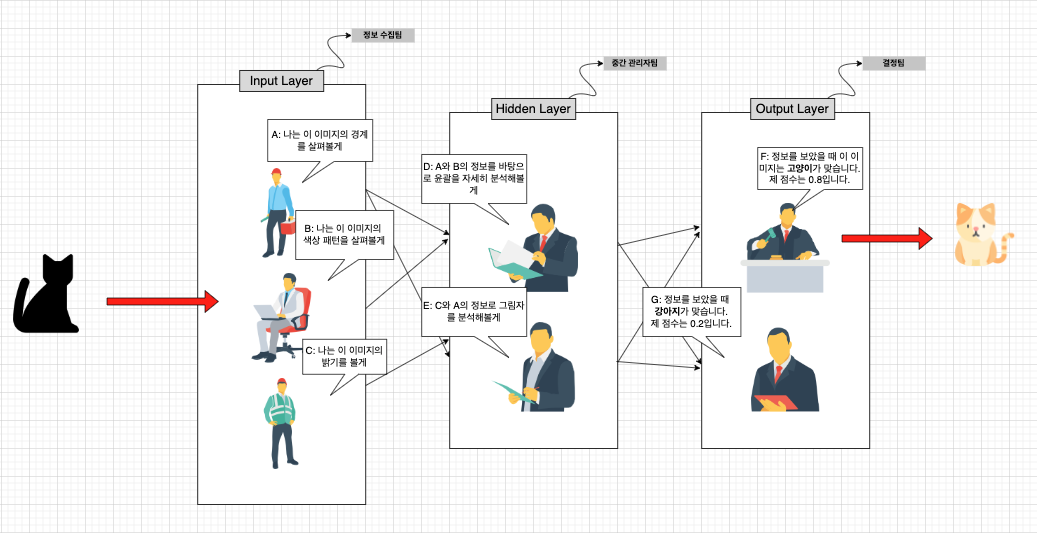
Input Layer(정보 수집 Team)
입력층은 데이터를 처음 받아들이는 층이다. 비유하자면, 이 층의 각 뉴런들은 특정 작업을 담당하는 사람들이 모인 팀이라고 생각할 수 있.
- A 뉴런은 "나는 이 이미지의 경계를 살펴볼게"라고 하며, 이미지에서 경계 부분을 분석한다.
- B 뉴런은 "나는 이 이미지의 색상 패턴을 살펴볼게"라고 하며, 색상 정보를 추출한다.
- C 뉴런은 "나는 이 이미지의 밝기를 볼게"라고 하며, 이미지의 명암을 분석한다.
이렇게 입력층의 뉴런들은 각각의 데이터를 분해하여 기본적인 정보(특징)를 분석한다.
Hidden Layer(중간 관리자 Team)
은닉층은 입력층에서 처리된 기본 정보를 기반으로 더 복잡한 특징을 학습한다. 은닉층을 중간 관리자들이 모인 팀으로 비유할 수 있다. 각 은닉층의 뉴런들은 입력층에서 나온 정보를 다시 조합해서 새로운 통찰을 얻는다.
- D 뉴런은 "A와 B의 정보를 조합해서 이 물체의 윤곽을 더 자세히 분석할게"라고 하며, 경계와 색상 정보를 결합해 물체의 형태를 더 정확히 파악한다.
- E 뉴런은 "C의 밝기 정보와 A의 경계 정보를 합쳐서 그림자와 물체의 관계를 분석할게"라고 하며, 명암과 경계를 이용해 물체의 3D 형태를 유추한다.
은닉층은 이렇게 여러 입력 정보를 조합하여 더 깊이 있는 특징을 학습합니다. 각 은닉층의 뉴런들은 입력층보다 더 추상적인 정보를 다루는 역할을 한다.
Output Layer(결정 Team)
출력층은 네트워크의 최종 결과를 내는 결정팀이다. 이 팀은 은닉층에서 처리된 정보를 바탕으로 최종 결론을 내린다.
- F 뉴런은 "이 정보를 종합했을 때, 이 물체는 고양이일 가능성이 가장 커"라고 결론을 내린다.
- G 뉴런은 "이건 새일 가능성이 높아"라고 판단한다.
출력층은 은닉층에서 처리된 복잡한 정보를 종합하여 최종 예측이나 분류 결과를 생성한다.
CNN에서 전이학습 방법
💡 전이학습이란?
기존에 학습된 모델을새로운 문제에 맞게 조금 수정해서 사용하는 것이다. 예를 들면 마치 축구를 잘하는 사람이 배구를 배울 때, 공을 다루는 기본 기술을 이미 알고 있으므로 새로운 스포츠도 더 빨리 익히는 것과 같은 것!
CNN을 사용할 때 우리 데이터를 처음부터 학습시킬 필요가 없다. 대신, ImageNet과 같은 대규모 데이터셋에서 이미 학습된 모델을 가져와서 그 가중치를 기반으로 새로운 데이터를 학습하면 된다. 이 과정을 파인튜닝(Fine-tuning)이라고 한다
과정
- ImageNet과 같은 큰 데이터셋에서 학습된 모델을 가져온다. 이 모델은 이미 다양한 특징(예: 이미지의 경계, 색상, 질감 등)을 학습한 상태이다.
- 우리의 데이터에 맞게 파인튜닝한다. 즉, 기존 모델의 가중치를 그대로 사용하면서, 마지막 몇 개 층만 교체하거나 수정하여 우리 데이터에 맞게 학습시킨다. 이렇게 하면 처음부터 모든 걸 학습시키지 않아도 되기 때문에 시간도 절약되고, 더 적은 데이터로도 좋은 성능을 낼 수 있다.
Activation Functions
💡 활성화 함수란?
신경망의 각 뉴런이 활성화할지 말지를 결정하는 함수이다.
신경망에서 뉴런이 입력을 받으면 이 입력을 계산해서 활성화 함수에 넘겨준다. 그리고 활성화 함수는 그 계산 결과를 비선형적인 형태로 변형해서 최종 출력값을 만든다.
쉽게 비유하자면, 뉴런은 마치 공장에서 제품을 조립하는 작업자이고, 활성화 함수는 포장지와 같다. 작업자가 재료(입력값)을 받아서 하나의 제품(가중치를 더한 합)을 생산하면 해당 제품을 바로 판매를 하는게 아니라 포장지로 포장해서 최종으로 판매하는 것이다.
💡활성화 함수의 기울기는 무슨 의미를 가질까?
활성화 함수의 기울기가 양수라면, 가중치를 낮춰 손실을 줄이고 / 음수라면, 가중치를 높여 손실을 줄인다.
[Sigmoid]
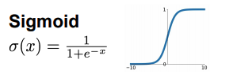
정의
입력값을 0과 1 사이로 압축하는 함수
좋은 점
1. 값이 [0, 1] 범위로 변환되어, 뉴런의 활성화율을 표현하는 데 유리하다.
2. 신경망에서 한때 많이 사용되었으며, 생물학적인 뉴런의 발화율을 모방할 수 있다.
문제 점
1. 포화 문제: 입력값이 매우 크거나 작은 경우, 출력이 0 또는 1에 가까워진다. 0 또는 1에 가까워지면 gradient는 0에 수렴하게 되어 학습이 거의 이루어지지않는 결과가 나오게 된다.
2. 0이 중심이 아님: 출력값이 항상 양수가 된다. 이때의 문제는 가중치가 한 방향으로 업데이트된다. 가중치가 한 방향으로만 업데이트되면 모델이 데이터의 복잡한 데이터를 잘 학습하지 못할 수있다.
3. 계산 비용: Sigmoid 함수는 e를 포함하고 있어 계산 비용이 상대적으로 크다.
[tanh]

정의
입력값을 -1과 1 사이로 압축하는 함수
좋은 점
0 중심 함수로, Sigmoid와 달리 출력이 -1에서 1 사이에 분포되므로 학습 시 더 효율적으로 작동한다.
문제 점
포화문제: Sigmoid 함수와 같이 입력값이 매우 크거나 작은 경우, 출력이 0 또는 1에 가까워진다. 0 또는 1에 가까워지면 gradient는 0에 수렴하게 되어 학습이 거의 이루어지지않는 결과가 나오게 된다.
[ReLU]

정의
음수 값을 모두 0으로 바꾸고, 양수 값을 그대로 통과시키는 함수
좋은 점
- 비포화성: 양수 입력에 대해 포화되지 않으므로, gradient가 0에 수렴하여 학습이 이루어지지 않는 결과를 막을 수 있다.
- 계산 효율성: 다른 활성화 함수들에 비해 매우 간단한 계산이기 때문에 빠르게 학습이 가능하다.
- 생물학적 타당성: ReLU는 뉴런이 일정 임계값 이상일 때 활성화되는 방식이 실제 신경망과 더 유사하다.
- 빠른 수렴: Sigmoid나 tanh에 비해 학습 속도가 훨씬 빠르다
문제 점
- "죽은" 뉴런 문제: 입력값이 0 이하일 경우 해당 뉴런은 항상 0을 출력하여 업데이트가 이루어지지 않는다. 이는 학습 초기에 많은 뉴런이 죽어 버리는 문제가 될 수 있다.
- 0 중심이 아님: 양수 영역에서만 활성화되기 때문에 출력이 0 중심이 아니며, 이는 학습에 불리할 수 있다.
❓ 왜 0 중심이 아니면 학습에 불리한가?
0이 중심이면 가중치가 양수와 음수로 자유롭게 변할 수 있어 양쪽으로 균형있게 학습이 가능하다. 하지만 0이 중심이 아니면 가중치가 항상 한쪽으로만 변해서 만약 반대 방향으로 가야하는 경우 학습을 제대로 할 수 없게 된다.
[Leaky ReLU]

정의
ReLU의 변형으로, 음수 입력에 대해 매우 작은 기울기(일반적으로 0.01)를 적용한다.
좋은 점
- "죽은" 뉴런 문제 해결: 음수 영역에서도 작지만 그래디언트가 존재하기 때문에 뉴런이 죽는 문제를 방지할 수 있다.
- 계산 효율성: ReLU와 비슷하게 계산이 효율적이다
- 빠른 수렴: ReLU와 마찬가지로 학습 속도가 매우 빠르다
❓ 빠른 수렴은 왜 학습 속도 빠름으로 이어지는건가?
수렴이라는 건 오차(손실 함수)가 점점 작아지면서 최적의 값에 도달하는 과정을 의미한다.
따라서, 빠른 수럼이란 신경망이 더 적은 시간이나 반복 안에 최저의 함수 값을 찾아낸다는 것을 의미 한다.
문제 점
0 중심이 아님: 양수 영역에서만 활성화되기 때문에 출력이 0 중심이 아니며, 이는 학습에 불리할 수 있다.
[Maxout]
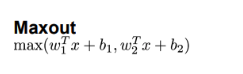
정의
여러 가중치로 이루어진 선형 함수들 중 가장 큰 값을 선택하는 함수
좋은 점
ReLU의 일반화: ReLU와 Leaky ReLU의 일반화된 형태로, 포화되지 않으며 뉴런이 죽지 않는다.
선형 구간: Maxout은 입력값에 대해 선형으로 반응하기 때문에 매우 강력한 표현력을 가진다.
문제 점
매개변수의 수가 2배로 증가하므로, 학습해야 할 파라미터가 늘어나고 계산 비용이 증가한다.
[ELU]
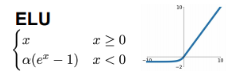
정의
ReLU의 변형으로, 음수 영역에서는 지수적으로 감쇠하는 값을 출력하고, 양수 영역에서는 ReLU처럼 작동하는 함수
좋은 점
0 중심 출력: ELU는 출력값이 0에 가까워질 수 있어, 0 중심 데이터 처리에 유리함.
강한 노이즈 저항성: 음수 영역에서 포화되는 특성 덕분에 잡음에 더 강함.
문제 점
지수 함수를 사용하므로, 계산 비용이 다소 큼.
❓Leakt ReLU vs ELU의 음수 영역 처리 방식의 차이점
Leaky ReLU: 음수 영역에서 기울기가 일정하게 유지되면서 간단하고 빠른 연산을 제공하지만, 비선형적인 변화는 적다.
ELU: 음수 영역에서 기울기가 일정하지 않고 지수 함수 형태로 변화하면서, 더 부드럽고 점진적인 학습을 가능하게 하고, 0 중심으로 학습이 이루어지도록 한다.
❗️왜 활성화 함수가 중요한가?
활성화 함수는 신경망이 단순한 계산을 넘어서 복잡한 패턴(비선형적 패턴)을 인식할 수 있도록 도와준다. 활성화 함수가 없다면 신경망은 그저 단순한 더하기와 곱하기만 가능하고, 비선형적 문제같은 복잡한 문제를 해결할 수 없게된다.
Data Preprocessing (데이터 전처리)
💡 데이터 전처리란?
데이터 전처리란 머신러닝 모델을 훈련하기 전에 원본 데이터를 정리하고 변환하는 과정이다.
원본 데이터에는 값이 비어있거나 다른 값들과 멀리 떨어져 있는 값이 있을 수 있다. 이런 값들 있으면 모델의 성능을 저하할 수 있어 데이터를 일정한 기준으로 변환하는 작업이 필수적이다.
❗️ 데이터 전처리의 필요성은 무엇인가?
데이터 전처리는 모델이 빠르고 정확하게 학습할 수 있도록 돕는다.
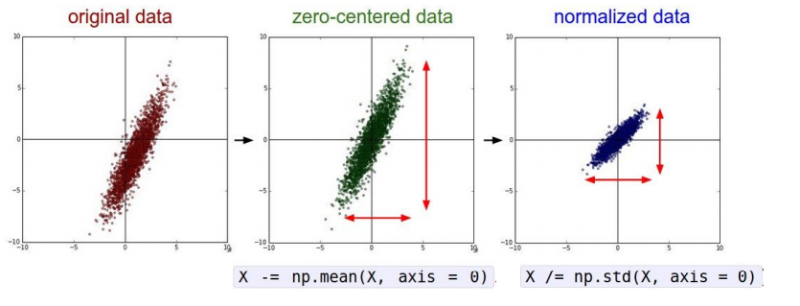
zero-centered data
데이터의 평균을 0으로 만드는 과정을 의미한다. 이렇게 하면 데이터가 더 쉽게 학습할 수 있다.
각 데이터에서 평균을 뺴서 데이터가 0을 중심으로 분포하도록 만든다. 예를 들어 어느 한 데이터들의 평균 값의 중심이 (3, 4)라면 x로 -3, y로 -4를 해서 데이터의 중심을 (0, 0)으로 맞추는 것이다.
normalized data- 이미지에서는 필요 없는 과정
데이터의 표준편차를 1로 맞추는 과정이다.
각 데이터에서 평균을 뺀 후, 표준편차로 1을 맞추는 과정이다. 즉, 특정 구간에 데이터를 모두 넣는 과정이다.
이미지에서는 이미 0~ 255 구간에 데이터가 모두 모여있기 때문에 정규화가 필요하지 않다.
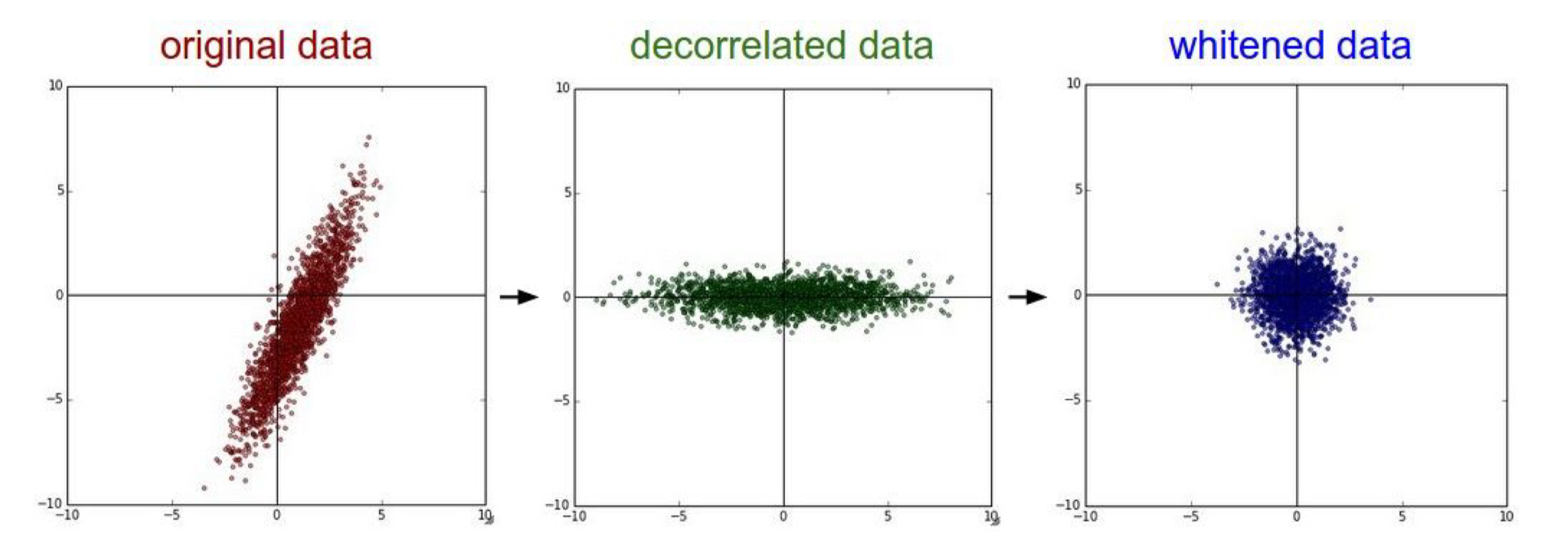
decorrelated data(PCA)
고차원 데이터를 더 낮은 차원으로 변환하면서 데이터 간 상관관계를 없애는 방법이다.
즉, 서로 연관된 데이터들을 다른 추긍로 돌려서 독립적인 데이터로 만드는 것이다. 이렇게 하면 데이터가 더 쉽게 분석되거나 모델이 학습하기 쉬워진다.
whitened data
데이터를 평균이 0이고, 모든 값들이 같은 규모(분산)를 가지도록 바꾸는 방법이다. 이건 데이터를 깨끗하게 만드느 과정이다.
즉, 모든 데이터들이 평균이 0이고, 값들이 똑같은 범위 안에 있게 맞추는 것이다. 이렇게하면 데이터들이 서로 너무 큰 차이가 없도록 만들어서 학습하기 더 좋다.
Weight Initialization (가중치 초기화)
잘못된 초기화의 문제
가중치가 0으로 초기화될 경우: 모든 뉴런이 동일하게 학습되므로 의미 없는 학습이 된다.
작은 난수로 초기화
방법: 0을 평균으로 하는 작은 가우시안 난수로 가중치를 초기화한다. 하지만 깊은 네트워크에서는 문제를 일으킬 수 있다.
❓ 왜 작은 난수로 초기화 하는 것이 깊은 네트워크에서 문제를 발생시키나?
우선 깊은 네트워크란 Hidden Layer가 많은 것을 의미한다.
가중치가 너무 작으면 데이터가 각 층을 지날 때마다 점점 작아져 결국 0이 되어 버리는 문제가 발생한다. 0이 되어 버리면 학습이 거의 되지 않거나, 학습 시간 매우 오래 걸리된다.
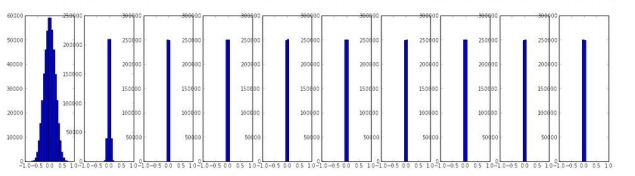
적당한 가중치를 설정하는 방법들
Xavier Initialization - sigmoid, tanh
정의: 신경망의 가중치를 너무 크지도, 작지도 않게 설정해 주는 방법
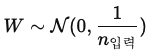
방법: 가중치를 랜덤하게 설정하지만, 그 값이 너무 크거나 너무 작아지지 않도록 적절한 범위 내에서 설정한다. (n 입력은 해당 층으로 들어오는 입력 뉴런의 개수) 즉, 입력 뉴런 개수에 맞춰 가중치 크기를 조정하는 것이다.
장점
소실된 gradient 문제 방지: 가중치가 너무 작지 않아서 신호가 점점 작어져 소실되는 문제를 방지해준다.
균형 잡힌 신호 흐름: 데이터가 네트워크를 통해서 지나갈 떄 일정한 범위 내에서 흘러가지 않도록 도와준다. 각 레이어에서 데이터가 지나가면서 신호가 너무 크거나 작지 않게 만들어준다.
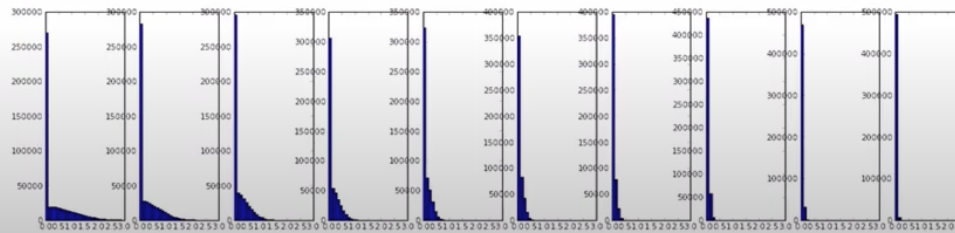
단점: ReLU와 같은 비선형 함수에는 적합하지 않다. 왜냐하면 ReLU는 양수만 통과시키는 특정이 있기 때문에 Xavier 초기화는 신호가 약해지게 만들 수 있다.
왜 양수만 통과시키면 Xavier 초기화는 적합하지 않을까?
Xavier 초기화는 양수와 음수를 대칭적으로 고르게 분포시키기 때문에 뉴런이 죽는 현상이 발생할 수 있기 때문이다.
따라서, 이 문제를 He 초기화로 해결해주었다.
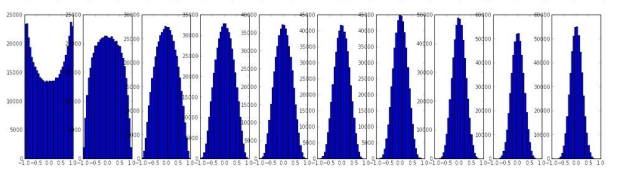
He Initialization - ReLU, Leaky ReLU
정의: Xavier 초기화보다 가중치 값을 좀 더 크게 설정해서 ReLU 함수의 특성에 맞춰 신호가 잘 흐르도록 돕는 방식
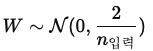
방법: Xavier 초기화와 방식은 비슷하지만 가중치를 조금 더 크게 설정한다. Xavier 초기화와 차이점은 1 대신 2를 사용하는 것이다. 이로 인해 신호가 너무 약해지지 않도록 더 큰 값으로 초기화된다.
장점
ReLU 활성화 함수와 궁합이 좋음: ReLU는 음수를 0으로 보내버리기 때문에, 가중치가 더 크면 신호가 사라지지 않고 잘 전달된다.
소실된 그래디언트 문제를 잘 해결: 특히, 깊은 네트워크에서도 그래디언트가 소실되지 않도록 가중치 값을 더 크게 초기화해 학습 속도가 빨라지고 안정적이다.
단점
ReLU 이외의 함수에서 부적합할 수 있음: 만약 ReLU가 아닌 시그모이드나 하이퍼볼릭 탄젠트 함수와 함께 사용하면 가중치가 너무 커져서 폭발하는 그래디언트 문제가 생길 수 있어.
가중치 초기화에 너무 신경 쓰지 않아도 되는 방법
우리는 손실된 그래디언트(Vanishing Gradient)를 방지하기 위해서 ReLU를 적용하거나, 가중치 초기화를 굉장히 신중하게 하는 방법으로 해결해왔다. 하지만 Bacth Normalization은 학습하는 과정 자체를 안정적으로 만드는 과정이다.
Batch Normalization
정의: 신경망이 학습할 때 각 레이어마다 데이터가 너무 커지거나 너무 작아지지 않도록 조정하는 방법이다.
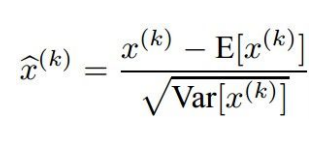
방법
- 정규화
- 각 mini batch에 대해 평균과 표준편차를 구한다.
- 그리고 그 데이터를 평균은 0으로 분산은 1로 마춰서 데이터가 너무 커지거나 작지 않도록 조정한다.
- 스케일링과 이동
- 데이터가 너무 단순해지면 신경망이 학습하기 어려우니, 다시 조금씩 조정한다. 이 때 크기 조정 값과 이동 값을 사용해서 데이터 크기를 조적당히 맞춰준다.
장점
- 가중치 초기화에 덜 신경 써도 된다.
- 데이터가 자동으로 정규화되기 때문에 가중치 최기화 문제에 덜 신경 써도 된다.
- 학습 속도 향상
- 데이터가 각 층에서 일정한 범위 내에 유지되기 때문에, Learining rate를 더 크게 설정해도 안전하게 학습할 수 있어, 학습 속도가 증가할 수 있다.
- 학습 안정성
- 각 층에서 신호를 정규화하기 때문에 gradient가 너무 작거나 커지는 문제를 줄여준다.
- 과적합 방지
- 어느 정도 규제 효과도 있어 간접적으로 과적합을 막는데 도움이 된다.
단점
- 추론 시 추가 계산이 필요하다.
- 학습할 때는 배치의 평균과 분산을 사용하지만, 실제 데이터를 입력받아 예측할 때(추론)에는 학습중 계산된 전체 데이터의 평균과 분산을 사용해야하기 때문에 추론 시 계산 비용이 조금 증가한다.
- 배치 크기에 민감하다.
- 너무 작은 배치 크기로 학습하면 평균과 분산의 계산이 불안정해질 수 있어, 배치 크기를 적절하게 조정해야한다.
- 순차 데이터를 적용하기 어렵다.
- Bacth는 순서를 중요하게 생각하지 않지만, 순차 데이터는 순서가 중요하기 때문에 데이터가 파괴될 수 있다.
Babysitting the Learning Process(학습 과정 관리)
: 모델 학습 과정에서 세세하게 관리하고 모니터링하는 것을 의미한다.
: 학습 중 발생하는 문제들을 실시간으로 확이하고, 이를 조정하면서 올바르게 학습하도록 돕는 과정이다.
- 데이터 전처리
- 데이터를 준비하는 과정이다
- 예를 들어, 이미지 데이터를 사용할 때, 크기를 조정하거나 밝기를 맞추는 것처럼 데이터를 정리하는 과정이다.
- 데이터가 너무 크거나 작은 값이 있으면 학습이 제대로 되지 않으니 0을 기준으로 값들을 정리하는 작업이 중요하다.
- NN 구조 결정
- 뉴럴 네트워크가 어떻게 생겼는지 설계하는 단계이다.
- 네트워크는 여러 층으로 이루어져 있고, 각 층에는 여러 개의 노드가 있어. 얼마나 많은 층을 만들지, 그리고 각 층에 몇 개의 노드를 둘지 결정해야한다.
- 가중치 초기화
- 모델 안에 있는 신경망들이 처음 시작할 때 어떤 값으로 시작할지를 설정하는 단계이다.
- 잘못된 값을 넣으면 학습이 어려워져서, 이 초기값이 중요하다. 너무 크거나 작은 값이 아니고 적절한 범위 내에서 초기값을 줘야한다.
- 초기 Loss 체크
- 학습이 시작되기 전에, 모델의 초기 성능을 확인하는 단계이다.
- 이때 Loss 값을 계산하고, 문제가 있는지 확인한다.
- 분류 문제에서는 softmax를 사용한 후 로그(Loss)를 체크하고, Loss 값이 제대로 계산되는지 확인해야한다.
- regularization을 사용하지 않으니, 여기서는 순수하게 초기 Loss 값만을 확인한다.
- 데이터 일부만 학습시켜보기
- 전체 데이터로 학습하기 전에, 데이터의 일부만을 사용해서 모델을 학습하면 모델이 잘 작동하는지, Loss가 적절하게 줄어들고 있는지를 확인할 수 있다.
- 이 때 과적합이 일어나면 역전파가 잘 되고, 가중치 업데이트도 잘되고 있다는 의미이다.
- 과적합이 일어나지 않는다면 무언가 잘못된 것
- Epoch마다 Loss와 Train Accuracy 확인
- 학습을 진행하면서, 각 Epoch(한 번의 학습 과정이 끝날 때마다)마다 Loss가 줄어드는지 확인해야 한다.
- 동시에, Train Accuracy(훈련 데이터에서의 정확도)도 함께 증가하는지 체크해야한다.
- Learning rate 설정
- Learning Rate는 모델이 얼마나 빠르게 학습할지를 결정하는 값이다.
- NaN(Not a Number)가 나온다는 것은 Learining rate가 너무 높다는 의미이다.
- 너무 작으면 학습 속도가 느려지고, 반대로 너무 크면 Loss 값이 갑자기 커지면서 모델이 학습을 제대로 못하게 될 수 있다. 적절한 Learning Rate를 찾아가는 게 중요하다.
- 보통 1e-3에서 1e-5 사이 값을 사용하지만, 모델에 따라 조금씩 다를 수 있다.
Hyperparameter Optimization
: 학습에 중요한 영향을 미치는 하이퍼 파라미터들을 적절히 설정하는 과정이다.
- Coarse Stage - 대략적으로 하이퍼 파라미터의 좋은 설정 값을 찾아보는 단계
- 먼저 넓은 범위에서 Learning Rate(모델이 얼마나 빨리 배우는지)나 Regularization(모델이 과적합하지 않도록 도와주는 값)을 너무 크거나 작지 않게 몇 번 설정해서 빠르게 Epoch(한 번의 학습 과정이 끝날 때마다)를 돌려본다
- 그 중에서 좋은 범위를 찾아야한다.
- [로그 스페이스]
- 범위를 정할 떄 정수 1, 2, 3 처럼 연속적으로 시도하는게 아니라 0.00001, 0.0001, 0.001처럼 차이가 나는 값들을 선택하는 방법
- 이렇게 해야 더 빠르게 좋은 범위 탐색이 가능하다.
- Fine Stage - 좀 더 세밀하게 값을 조정해보는 단계
- 처음에 적당히 맞춰본 범위 중에서 더 정확하게 어떤 값이 좋은지를 찾는 단계
- 이 과정에서 Cost(손실)가 더 커지거나 학습이 제대로 안 되는 경우, NaNs가 발생할 수 있다. 만약 Cost가 갑자기 크게 증가하면 학습이 불안정하다는 신호이니, 다른 하이퍼파라미터 설정으로 변경해야 한다.
- 💡NaNs란 뭔가?
- 숫자가 너무 이상하게 커지거나 계산이 잘못될 때 나오는 오류
- Regularization 범위와 Learning Rate 범위 정하기 - 모델이 잘 배우고 과적합 되지 않도록 적당한 값을 찾는 단계
- Regularization 범위: Regularization은 모델이 너무 학습 데이터에만 맞춰서 외울 때(과적합) 방지하는 값이다.
- 처음에는 0.0001, 0.001, 0.01 이런 식으로 큰 값에서부터 시작해 범위를 좁혀 나가는 게 좋다.
- Learning Rate 범위: 모델이 얼마나 빨리 배우는지를 결정하는 값이다.
- Learning Rate가 너무 크면 모델이 제대로 학습을 못하고, 너무 작으면 학습이 너무 느리다.
- Learning Rate는 0.001에서 0.0001 사이 값들이 자주 사용된다.
- Regularization 범위: Regularization은 모델이 너무 학습 데이터에만 맞춰서 외울 때(과적합) 방지하는 값이다.
- 범위의 중앙값에 최적 값이 오도록 설정하기
- Coarse Stage에서 넓은 범위를 시도해보고 나면, 어느 정도 좋은 값이 나오는 범위가 좁아진다.
- 그 범위의 중앙값을 기준으로 더 세밀하게 탐색하는 것이다.
- 이렇게 하면 최적의 Learning Rate나 Regularization 값을 더 쉽게 찾을 수 있다.
- Random Search 사용
- 하이퍼파라미터(모델이 학습할 때 정해진 값들)를 최적화할 때 모든 경우를 하나씩 시도하는 대신에 여러 값을 무작위로 선택해서 시도하는 방법이다.
- 이 방법을 쓰면 시간이 덜 걸리고, 더 다양한 값들을 시도해볼 수 있다
- Loss Curve 설명 - 학습 중에 Loss 값이 잘 줄어드는지 확인하는 단계
- 학습 중에는 Loss Curve(손실 그래프)를 계속 봐야 한다.
- 보통 처음에는 천천히 줄어들다가, 어느 순간 빠르게 줄어들어야 한다. 그런데 처음에 너무 변화가 없다가 갑자기 빠르게 내려가면 초기화 문제일 수 있다.
- Train Accuracy와 Validation Accuracy의 차이 - 차이가 크면 과적합 방지 / 차이가 없으면 더 복잡한 모델로 확장가능
- Train Accuracy는 훈련 데이터에서 모델이 얼마나 잘 맞추는지, Validation Accuracy는 새로운 데이터에서 얼마나 잘 맞추는지
- 차이가 크면?: 두 값이 크게 차이 나면, 모델이 훈련 데이터에 너무 맞춰져서 외우고 있는 거다. 이때는 Regularization을 더 강하게 해서 모델이 과적합되지 않도록 해야 한다.
- 차이가 없으면?: 두 값이 비슷하다면 과적합이 일어나지 않고 잘 학습하고 있다는 뜻이다.
- 가중치 업데이트 비율과 가중치 크기
- 가중치가 학습하면서 조금씩 업데이트한다. 이때 가중치 크기에 비해 업데이트 비율이 적절해야 모델이 안정적으로 학습할 수 있다.
- 가중치 크기 구하기: 가중치 크기는 모델 파라미터의 크기를 수치적으로 구한 값이다.
'CVLab > cs231n (2016)' 카테고리의 다른 글
| cs231n - lecture07(CNN) (0) | 2024.10.01 |
|---|---|
| cs231n - lecture06(Trainit NN Part 2) (0) | 2024.09.28 |
| 2024.09.27 Q&A (1) | 2024.09.27 |
| cs231n - lecture04(역전파, 신경망) (0) | 2024.09.27 |
| cs231n - lecture03(손실함수, 경사하강법) (1) | 2024.09.23 |



