Data Augmentation (데이터 증강)
: 원본 이미지를 변형하는 과정을 추가하여, 모델의 성능을 증가시키는 방법이다. 즉, label을 변하지 않고 label의 pixel의 값을 여러 형태로 변형 시켜 모델을 학습시키는 것이다.
Horizontal flips(수평 뒤집기)
: 이미지 좌우를 뒤집는 간단한 방식
Random crops / scalse(무작위 자르기 및 크기 조정)
: 이미지를 무작위로 자른 후 일정한 크기로 맞추는 방식

ResNet에서는 아래와 같은 방식을 사용했다.
[이미지 생성]
1. [256, 480] 사이의 하나의 수를 골라 이를 L이라고 한다. (이 때, L은 width와 height 둘 중 하나로, 더 짧은 쪽의 길이를 의미한다.)
2. 학습시킬 이미지를 이 L을 기준으로 resize해준다.
3. 이 resize된 이미지로 부터 224x224의 패치를 랜덤하게 10개정도 샘플링 해준다. (이 때, 224x224x는 ResNet에 input으로 들어가는 사이즈이다.)
이처럼 Data Augmentation을 이용하면, 학습 시 이미지 전체에 대한 학습이 아니라, 이미지의 어느 부분에 대한 학습이 이루어지기 때문에 테스트를 하는 경우에도 이미지의 정해진 부분을 통해서 테스트를 진행하게 된다.

[테스트]
1. 테스트할 이미지를 5개의 크기로 resize해준다. (224, 256, 384, 480, 640)
2. 각각의 사이즈에 대해 224x224의 크기를 가지는 10개의 crop을 만들어준다.
(코너 부분의 crop 4개 + 중심 부분의 crop 1개 = 5개) ☞ 이를 crop이 10개이기 때문에 총 50개가 만들어진다.)
3. 이 50개에 대해 평균을 구해준다.
Color jitter(색상 왜곡)
: 이미지의 색상 대비나 채도를 무작위로 변경하는 방식
Simple Version
: 대비를 조정한다.
Complex Version
1. R, G, B 각각에 PCA를 적용한다. (R, G, B 채널 간의 상관관계를 고려해서 색상을 변형하는 기법이다.)
좀더 자세하게 말하자면 아래와 같다.
2. 주성분 방향에 따라서 색상을 샘플링한다.
: PCA가 찾아낸 중요한 색상 변화 방향에 따라서, 무작위로 색상 offset(변화량)을 선택한다. (색상을 어떻게 바꿀지 결정하는 요소)
3. 색상 변화를 이미지에 적용한다.
: 선택한 색상 변화량을 이미지의 모든 픽셀에 적용하여, 이미지 전체의 색상을 조금씩 바꾼다. 이렇게 하면 원래 이미지에서 색상이 약간 변한 이미지를 만들 수 있다.
- RGB 채널 간 상관관계: 이미지의 각 픽셀은 R G B를 가지며, 이 채널들 간에 상관관계가 있을 수 있다. 예를 들어 밝은 이미지는 새 채널 모두에서 높은 값을 가질 수 있다.
- PCA 적용: 각 채널 픽셀 값들을 하나의 벡터로 보고 PCA를 수행하여 가장 중요한 주성분 방향(패턴)을 찾는다. 예를 들어, 어떤 이미지에서는 R, G가 자주 강하게 나오고, B는 덜 나오는 패턴이 있을 수 있다. PCA는 이런 패턴을 찾아서 주성분이라는 중요한 축을 만든다.
- 색상 왜곡: 찾은 주성분 방향을 기준으로 무작위 색상 변화를 준다. 쉽게 말해서, 이 축을 R, G, B 각 채널을 모두 한 번에 살짝씩 바꾸는 것이다.
Get creative(창의적인 변형)
: 회전, 이동, 왜곡 등을 통해서 더 많은 변형 데이터를 만드는 방식
Data Augmentation의 General Theme
Training
데이터를 학습할 때 랜덤 노이즈를 추가한다. 이렇게 하면 모델이 다양한 상황에서 더 일반화를 잘 수 있도록 도와준다.
Testing
테스트 시에는 노이지를 평균화하여 더 안정된 예측을 할 수 있도록 한다.
위처럼 생각한다고 가정하면 Dropout(일부 node OFF), DropConnect(node간의 연결 일부 disconnect), Batch normalization, Model ensembles과 같은 경우에도 Data Augmentation과 같은 효과를 얻는다고 생각할 수 있다.
종합적으로, Data Augmentation는 구현하기가 쉽게 때문에 사용하는 것을 추천하고 dataset의 크기가 작은 경우 더 유용하다.
Data Augmentation는 학습 시에는 노이즈를 더해주고, 테스트 시에는 노이즈를 평균화하는 프레임 워크이다.
Transfer Learning (전이 학습)
: 이미 학습된 모델을 이용해서 내가 원하는 분류기로 수정하는 과정

1번처럼 새로운 모델을 학습시킬 때 다시 새롭게 학습 시킬 필요가 없다.
[small dataset]
만약 imageNet처럼 큰 데이터 셋으로 이미 잘 학습된 모델이 있을 때, 작은 데이터 셋을 이용해 학습을 시키려면 전부 다시 학습할 필요가 없다. 이미 잘 학습된 모델의 대부분을 그대로 사용하고, 마지막 부분만 새로 학습하면 된다. 이 때 모델의 앞부분은 Feature Extractor처럼 작동하는데, 이미지에서 중요한 특징들만 뽑아내는 역할을 한다. 그래서 FC1000과 softmax 부분만 새 데이터에 맞춰서 다시 학습을 시켜 원하는 결과는 얻는다.
❓왜 FC와 softmax만 학습을 다시 시키는 걸까?
: 이미지에서 가장 기본적인 특성(선이나 모서리)은 대부분 이미지에서 공통적으로 나타나기 때문에, 이 레이어들은 데이터 셋에서 일반적으로 잘 동작한다. 따라서 굳이 다시 학습시킬 필요가 없다. FC와 softmax 레어들은 앞에서 추출된 특징들을 바탕으로 특정한 분류 작업을 한다. 따라서 우리는 이미 학습된 모델로 우리가 원하는 분류기를 만들기를 원하기 때문에, FC와 softmax를 다시 학습 시켜 우리가 원하는 카테고리와 그 카테고리의 수를 조정할 수 있다.
[medium dataset]
데이터셋이 좀 더 큰 경우에는 앞 부분도 전부 고정하지 않고 일부는 학습을 더 하게 만든다. 데이터가 더 커지면 커질수록 고정하는 부분을 줄여가면서 네트워크의 더 많은 부분이 새 데이터를 학습할 수 있게 한다. 즉, 처음에는 마지막 부분만 학습시키다가 점차 네트워크의 앞부분도 학습을 시켜 전체 성능을 개선시키는 방식으로 진행한다. (파인 튜닝)
❓ 이전 학습을 통해서 새로운 모델을 학습시킨다는 것이 어떻게 새로운 모델 성능 향상에 쉽게 도움을 줄 수 있을까?
경우 1) 이미지 셋에 있는 카테고리들과 비슷한 이미지를 분류할 때
: FC와 softmax만 다시 학습을 한다. ➡️ 이미 분류하려는 카테고리에 대한 모델이 만들어져있기 때문에
경우 2) 이미지 셋에 있는 카테고리들과는 무관한 이미지(의료 이미지 같은 것)를 분류할 때
: conv-64 부분을 제외하고 나머지를 다시 학습시킨다. ➡️ conv-64는 선과 모서리, 색상에 대한 특징을 인식한다. 이런 특징을 어떤 이미지에도 있기 때문에 미리 특징 인식하는 레이어를 만들어 놓으면 도움이 된다.
| 데이터의 수 \ 데이터 유사성 | 기존 데이터 셋과 비슷한 데이터 | 기존 데이터 셋과 다른 데이터 |
| 작은 데이터 | 최상단 레이어에만 선형 분류기를 적용한다. 앞 부분은 이미 잘 학습되어 있어서 마지막 분류기 부분만 바꿔도 된다. | (상황에 따라서 어디까지 고정하고 어디까지 학습 시켜야하는지 결정해야한다.) 다양한 레이어에서 다른 단계를 시도하면서 선형 분류기를 적용해야한다. 이 방법은 어떤 레이어가 새로운 데이터에 적합한 특징을 잘 추출하는지 확인하기 위함이다. |
| 큰 데이터 | 기존 데이터 셋의 일부 레이어를 파인튜닝할 수 있다. 유사한 데이터이기 때문에 완전한 재학습이 필요 없고, 모델의 일부만 학습을 진행해서 성능을 개선할 수 있다. | 더 많은 층을 파인튜닝해야한다. 새로운 데이터 셋이 기존 데이터 셋과 다르기 때문에, 모델이 처음부터 끝까지 더 많은 레이어를 다시 학습해서 새로운 특징을 추출하도록 해야한다. |

전이학습은 객체탐지(Faster R-CNN)과 이미지 캡셔닝에서 기본적으로 사용된다.
객체 탐지에서는 이미지에서 물체를 찾아내고 분류하는데 사용되고, 이미지 캡셔닝에서는 이미지를 설명하는 문장을 생성하는데 사용된다.
All About Convolutions: #1 How to stack them?(어떻게 쌓느냐?)
❓ 합성곱이란?
: 필터가 이미지 위를 이동하면서 여러 위치에서 부분적으로 곱한 값을 더하는 연산이다. 즉, dot product의 결과가 행렬로 만들어지는 것.
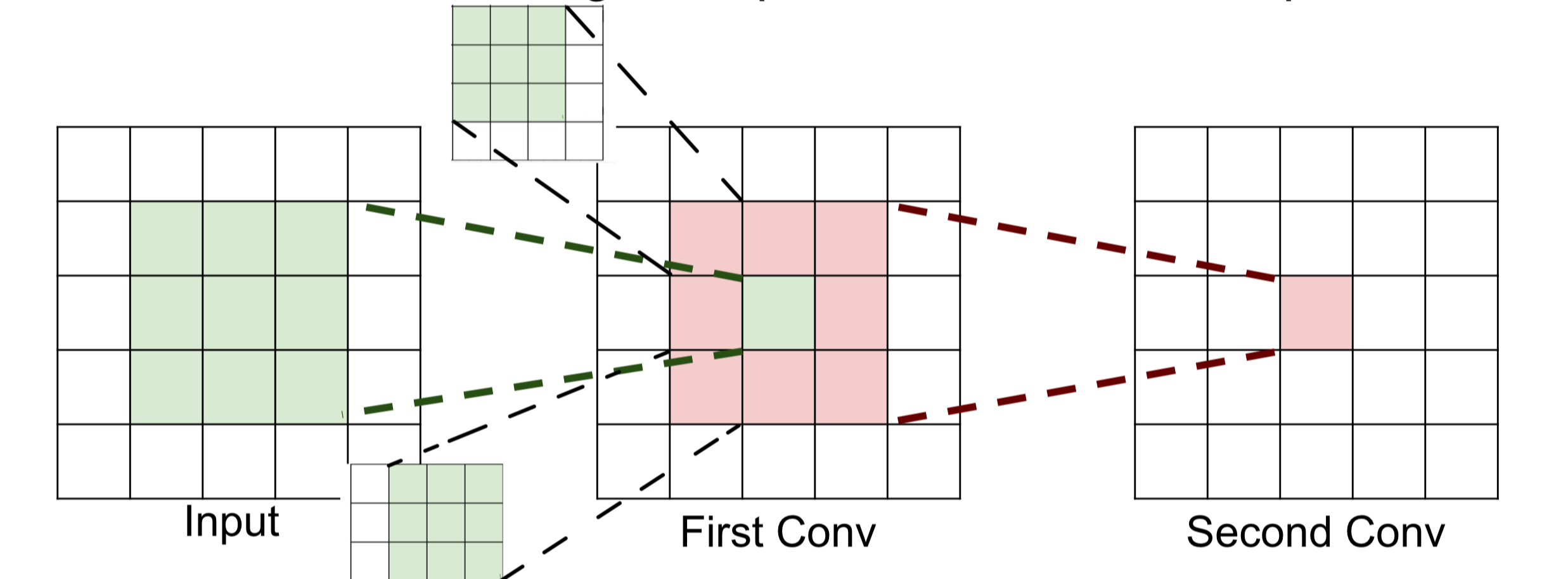
First Conv - Feature map의 한 구역은 Input의 3x3이고, Second Conv - Feature map의 한 구역은 Firtst Conv - Feature map의 3x3이고, input의 5x5이다.
Quiz) Second Conv의 하나의 구역은 input의 몇개의 구역일까?
: 5x5이다.

Quiz) 만약 third Conv의 하나의 구역은 input의 몇개의 구역일까?
: 7x7이다.
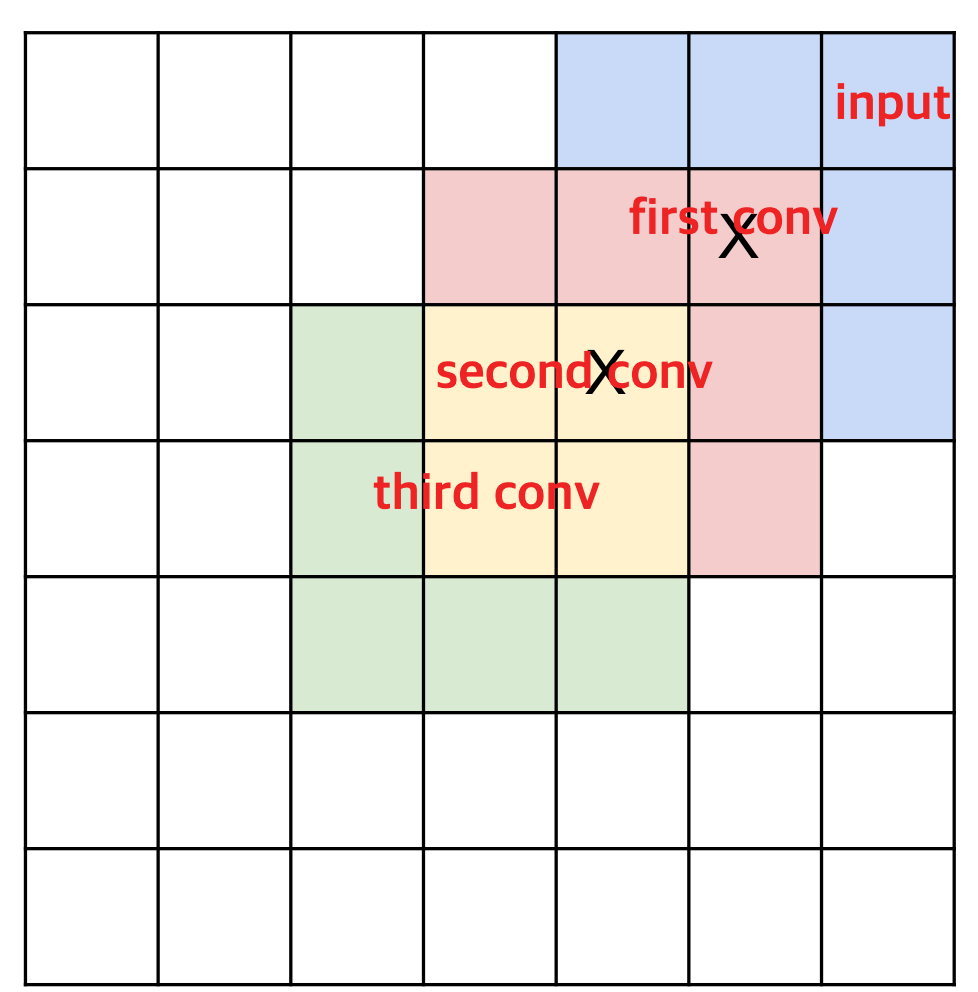
따라서 3x3 conv(필터) 3개는 7x7 conv(필터) 1개와 같은 효과를 지닌다. (직관적으로 만)
32x32x3의 인풋이 있고, 5x5, stride는 1, padding은 2인 필터가 10개 있을 떄 파라미터의 값은? (파라미터 값이란, 가중치와 bias를 뜻한다. 즉, 각 필터의 가중치 값들이 특정 패턴(엣지, 질감, 모양 등)에 민감하게 반응해 그 특징을 이용해 featrue map을 만든다. )
필터의 크기가 5x5이고, input의 depth는 3이기 때문에 5 * 5 * 3 = 75이다. 그리고 각 필터는 bias 항 하나를 가지기 때문에 75 + 1 = 76이다. 따라서 이러한 필터가 총 10개 있기 때문에 76 * 10 = 760이다.
그렇다면, H x W x C의 인풋이 있고 C개의 필터가 있을 때 7x7필터가 있는 ConvLayer가 1개인 경우와 3x3 필터가 있는 ConvLayer가 3개인 경우의 매개변수의 개수는?
우선 7x7의 경우에는 7 * 7 * C(depth) * C(filter) * 1(Layer) = 47C²이고,
3x3의 경우에는 3 * 3 * C(depth) * C(filter) * 3(Layer) = 27C²이다.
이 연산 결과의 의미는 3x3필터가 있는 ConvLayer를 사용하는 경우가 더 적은 매개변수가 필요하고, 3개의 Layer를 거치기 때문에 중간중간에 있는 활성화 함수로 좀더 비선형적 패턴에 강하다는 장점이 있다.
이렇게 작은게 더 좋은 결과를 낸다면 1x1이 제일 좋은걸까?
1x1 필터는 계산량을 줄이고 depth를 조합하여 새로운 특징을 만드는 것에는 유리하지만, 1x1필터는 같은 위치의 depth 간의 관계만 조합하기 때문에, 주변 픽셀 간의 관계를 학습할 수 없어서 공간적 패턴(모서리, 모양 등)을 인식할 수 있는 능력이 부족하므로 다양한 크기의 필터와 함께 사용한다면 좋은 성능을 얻을 수 있다!!!
예를 들면 Bottleneck sandwich(1x1 필터를 사용해 채널 수를 줄이고, 이후에 더 큰 필터(예: 3x3)를 사용한 다음, 다시 1x1 필터로 마무리하는 구조) 같은 형태이다.
하지만, 현재까지도 3x3 필터를 사용해야한다. 3x3크기를 좀더 줄일 수 없을까?
바로 3x1, 1x3 형태로 필터를 만들어서 특징맵을 찾는다면 좀더 적은 가중치의 개수를 사용해서 특징 맵을 추출할 수 있다.

이렇게 실제 값을 비교해봐도 단순하게 3x3 형태의 필터만 사용하는 것과 차이가 나게 된다.
이러한 방식은 GoogLeNet에서도 사용된다.
요약하자면, 5x5, 7x7과 같은 큰 크기의 필터를 사용하기보다는 3x3과 같은 작은 필터 여러개를 사용하는 것이 더 가중치를 적게 사용할 수 있고, 3x3도 그냥 사용하는 것이아니라 1 x n , n x 1과 같은 형태로 사용하는 것이 더 적은 연산과, 더 많은 비선형 패턴을 학습하게 할 수 있다..
All About Convolutions: #2 How to compute then?(어떻게 연산을 하느냐?)
❓합성 곱이란?
: 필터가 입력 이미지위를 슬라이딩하면서 각 위치에서 dot product를 수행하는 것
❓행렬 곱셈이란?
: 필터가 입력 이미지 전체를 한번에 dot product 수행하는 것
현재 다양한 플랫폼에서 최적화된 행렬 곱셈 알고리즘이 존재한다. 그래서 합성 곱연산을 행렬 곱셈으로 변환하면 연산속도와 효율성을 극대화 할 수 있다. 따라서, im2col(image to column)기법을 사용하면, 입력 이미지를 패치 단위로 변환하여 행렬 곱셈형태로 처리할 수 있게 된다.
image2col
예를 들어 9x9 이미지와 3x3 필터(stride = 1)가 있다고 해보자.
1. 이미지와 패치 나누기
: 이미지를 슬라이딩 했을 때 필터크기의 이미지 일부가 패치이다. 따라서, 이 이미지를 슬라이딩 하는 경우 3x3 크기의 49개 패치가 나오게 된다. 즉, 7x7 패치이다.
2. 각 패치를 벡터로 펼치기
: 각 3x3 패치를 1차원 벡터로 펼친다. 즉, 각 패치는 9x1 형태의 벡터가 된다. 그러면 9x1 형태의 벡터 49개가 된다.
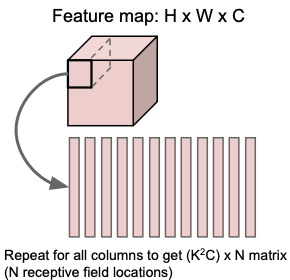
3. 전체 패치를 행렬로 구성하기
: 이제 49개의 9x1 패치를 하나의 큰 행렬로 모은다. 이 행렬은 49x9형태가 되고, 각 행은 하나의 3x3 패치를 1차원으로 펼친 것이다.

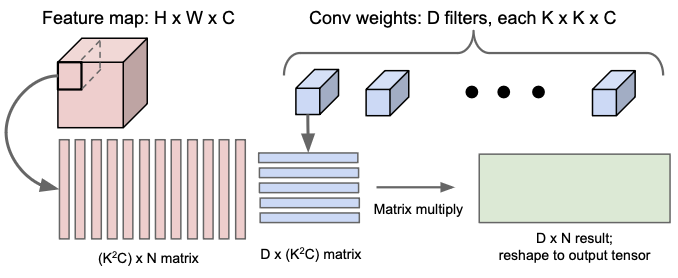
4. 필터도 1차원으로 변환하기
: 3x3 필터도 1차원 벡터로 펼쳐 9x1로 만든다. 만약 필터의 개수가 N개 라면, 각 필터를 9x1xN으로 9xN형태로 구성할 수 있다.
5. 행렬 곱셈 수행하기
: 이렇게 모인 49x9 패치 행렬과 9x1(또는 9xN)을 곱하면, 각 패치와 필터의 dot product 결과가 나온다. 이 결과는 49x1(또는 49xN) 크기의 행렬이 되고, 이 값을 다시 7x7로 재구성하면 최종 합성곱 연산결과인 feature map된다.
(아래의 이미지에서 D x (K²C)가 앞으로 와서 연산이 되어야한다. 즉, D x (K²C) · K²C x N으로 순서가 바꾸어야한다.
따라서, D x (K²C) · K²C x N = D x N)
FFT(Fast Fourier Transform)
❓Fourier Transform(푸리에 변환)이란?
: 이건 수학적인 방법인데, 이미지 같은 데이터를 "주파수"라는 다른 방식으로 표현하는 것이다. 쉽게 말하면, 이미지를 "다른 언어"로 바꾸는 과정이라 생각하면 된다. 이 방식을 사용하면 곱셈 연산이 더 빠르게 수행될 수 있다.
왜 FFT를 사용하는가?
합성곱은 이미지의 여러 부분을 한번에 스캔하면서 연산을 수행하는데, 이 과정이 복잡하고 시간이 오래걸릴 수 있다. 특히, 필턱 크거나 임지가 클수록 더 느려진다.
FFT를 이용한 합성곱 방식
1. 필터와 이미지를 주파수(새로운 언어)로 바꾸기
: FFT를 사용해 필터와 이미지를 푸리에 변환한다.
➡️ 필터의 푸리에 변환 𝐹(𝑊)을 계산한다.
➡️ 필터의 푸리에 변환 𝐹(X)을 계산한다.
2. 푸리에 변환한 두가지를 곱하기
: 필터와 이미지의 푸리에 변환 결과를 각각 곱한다.
➡️ 필터와 이미지의 푸리에 변환 결과들을 원소별로 곱한다. 𝐹(𝑊) · 𝐹(X)
3. 다시 원래 이미지(원래 언어)로 돌아가기
: 최종적으로 곱셈 결과를 역 푸리에 변환을 하여 원래 이미처럼 해석 가능한 형태로 되돌린다.
➡️ 마지막으로, 역 푸리에 변환 F⁻¹ ( 𝐹(𝑊) · 𝐹(X))을 수행하여 최종 합성 곱 결과 Y를 얻는다.
결과적으로 필터의 크기에 따라서 속도 향상이 되는 부분이 많아지는 것을 볼 수 있다.(초록색 부분이 속도가 향상되는 부분이다.)

Fast Algorith(합성곱 연산을 더 빠르게 수행하기 위한 다양한 알고리즘)
빠른 행렬 곱셈 알고리즘을 합성곱에 적용하기(Strassen’s Algorithm)
일반적으로 행렬 곱셈을 직접 수행할 경우, 두 NxN 크기의 행렬을 곱하려면, 연산 복잡도 O(N³)를 가진다. 즉, 행렬의 크기가 커질수록 계산량이 급격하게 증가하기 때문에 이 방식은 비효율적이다.
이때 사용할 수 있는 방식이 Strassen’s Algorithm이다. 이 알고리즘은 기존의 방식과 다른 수학적 계산법을 적용하여, 연산 복잡도를 O(N ².⁸¹ )로 줄인다. Strassen’s Algorithm은 합성 곱 연산에서도 계산량을 줄이는데 효과적이며, CNN처럼 수많은 합성곱 연산이 필요한 모델에서 유용하다.
3x3 합성곱에 특화된 최적화 방법(Lavin과 Gray)
Strassen’s Algorithm의 방식이 일반적인 행렬 곱셈의 효율을 높이는 데 초점을 맞춘다면, Lavin과 Gray는 특히 3x3 합성곱에 특화된 최적화 알고리즘을 제안했다. CNN에서 많이 사용하는 3x3 필터는 이미지의 작은 특징을 추출하는 데 유리하기 때문에 3x3 필터에 특화된 알고리즘이 필요하다.
Lavin과 Gray의 최적화 방법은 3x3 합성곱을 수행할 때 계산량을 줄일 수 있는 특수한 수학적 기법을 적용하여, 이전 방식보다 빠르게 결과를 얻을 수 있도록 설계되었다. 이 방법은 CNN 모델, 특히 VGG 같은 구조에서 자주 사용되는 3x3 필터 연산을 더 효율적으로 수행하게 해준다.
VGG 모델에서 Lavin과 Gray 알고리즘의 성능 향상

VGG모델은 3x3 필터를 여러 층에서 사용하기 때문에, 이 최적화 방법이 큰효과를 발휘할 수 있다. 표에 나와있는 Speedup 수치는 일반적인 합성곱 연산에 비해 얼마나 더 빨라졌는지를 나타낸다. 특히, VGG 모델과 같이 작은 배치로 연산할 때 이 알고리즘이 큰 성능 향상을 제공하는 것을 알 수 있다.
따라서 위의 내용들을 총 요약하면 아래와 같다.
im2col: 큰 메모리 오버헤드가 생기지만, 구현이 쉽다.
FFT: 작은 필터에 대해서는 큰 속도 향상을 얻을 수 있다.
Fast Algorithms: 작은 필터에 큰 속도 향상을 얻을 수 있지만, 특정 조건에 특화되어 있어 아직 널리 사용하지는 않는다.
Implementation Details (구현 세부 사항)
해당 내용을 옛날버전의 내용이라 생략했습니다.
Floating Point Precision(부동소수점 정밀도)와 그로 인해 발생할 수 있는 문제와 해결 방안
부동 소수점 정밀도는 딥러닝에서 중요한 개념이다. 이는 컴퓨터가 소숮머 이하의 값을 얼마나 정확하게 처리할 수 있는지에 대한 기준으로, 일반적으로 딥러닝 연산에서 기본으로 사용하는 정밀도는 32bit이다. (64bit를 사용하지 않는 이유는 딥러닝 모델 학습에 필요한 수학적 연산은 대부분 수치적인 근사값을 필요하기 때문에 32bit로도 충분한 정밀도를 얻을 수 있기 때문이다.)
하지만, 32bit는 높은 정밀도를 제공하지만, 연산량이 많고 메모리 사용량이 커서 딥러닝 모델을 학습하는데 제약이 있을 수 있다.
그래서 최근에는 16bit를 많이 사용하고 있다. 32bit보다 정밀도는 낮지만, 연산 속도가 빠르고 메모리 효율이 높아서 GPU에서 특히 유리하다. 그러나 16bit를 사용할 경우, 숫자가 매우 작거나 매우 큰 값에서 정밀도 손실이 발생할 수 있고 이런 오차들이 모여 모델 학습에 부정적인 영향을 미칠 수 있다.
이를 해결하기 위해서 Mixed Predcision Training이라는 기업이 사용된다. Mixed Predcision Training은 정밀도가 중요한 연산은 32bit가 처리하고, 나머지 연산은 16bit로 처리를 하여 속도와 메모리 효율을 극대화하면서도 학습을 안정화하는 방식이다. 이때도 매우 작은 값들이 손실되지 않도록 Loss Scaling이라는 기술을 활용하는데, 이는 작은 값을 확장해서 연산한 후 다시 축소하는 방식으로 수치 오차를 방지한다.
여기에 더해서, 낮은 정밀도로 인한 오차 문제를 줄이기 위해 Stochastic Rounding(확률적 반올림) 기법을 사용할 수 있다. 일반적인 반올림에서는 소수점 자릿수에 따라 고정된 기준으로 반올림하지만 Stochastic Rounding은 값이 반올림 기준에 근접할 때 확률적으로 반올림하거나 내림하여 정밀도 손실을 최소화하는 방식이다. 예를 들어, 3.6이라는 값이 있을 때, 일반 반올림은 항상 4로 올리지만, Stochastic Rounding은 60% 확률로 4로 올리고, 40% 확률로 3으로 내리는 식으로 평균적으로 더 정확한 값을 유지하게 한다.
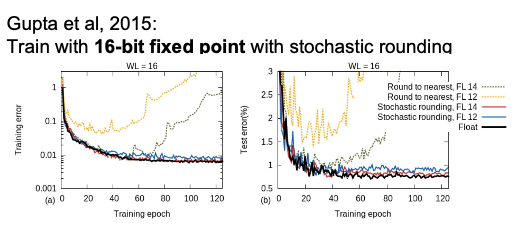
GPU는 16bit 연산에 최적화되어 있어, Mixed Precision Training을 활용하면 더 많은 데이터를 한 번에 처리할 수 있으며, 메모리 사용량을 줄여 모델 학습 속도를 높일 수 있다. 특히 최신 GPU 아키텍처에서는 16bit와 같은 낮은 정밀도를 매우 빠르게 처리할 수 있도록 지원하고 있어, 모델을 더 큰 배치로 학습하거나 더 복잡한 모델을 학습하는 데 큰 장점이 된다.
결론적으로, 부동 소수점 정밀도는 딥러닝 모델의 성능에 중요한 영향을 미친다. 그래서 밀도가 중요한 연산은 32bit가 처리하고, 나머지 연산은 16bit로 처리를 하는 Mixed Predcision Training은 정밀도와 연산 속도 간의 균형을 맞추며, 딥러닝 모델의 학습시간을 단축하고 자원을 더 효율적으로 활용할 수 있게 한다. 또한, Stochastic Rounding을 통해 낮은 정밀도로 인한 오차 누적을 줄여 수치적 안정성을 더욱 높일 수 있다.
'CVLab > cs231n (2016)' 카테고리의 다른 글
| 2024.11.07 Q&A (0) | 2024.11.09 |
|---|---|
| 2024.10.11 Q&A (1) | 2024.10.11 |
| cs231n - lecture10(RNN) (1) | 2024.10.09 |
| cs231n - lecture09(CNN의 시각화 및 이해) (5) | 2024.10.06 |
| 2024.10.04 Q&A (0) | 2024.10.04 |



