💡 특징 공간: 데이터의 특성을 나타내는 변수들로 이루어진 공간
2차원 특징 공간
1차원 특징 공간과 다르게 2차원 특징 공간은 두개의 x축을 통해서 y축을 예측하는 것이다.
따라서, 2차원에서의 특징 벡터 x는 (x₁, x₂)ᵀ 방식으로 표현할 수 있다. 이를 바탕으로 키, 몸무게에 대한 장타율을 나타내면 아래와 같다.

다차원 특징 공간
2차원 뿐만 아니라 그 이상 차원에서도 특징 벡터를 표현할 수 있는데 다차원에서의 특징 벡터 x는 (x₁, x₂, x, x, ..., xd)ᵀ 방식으로 표현할 수 있다.


특징 공간 변환과 표현 학습

위와 같이 직선으로 분류할 수 없던 특징 공간을 분류할 수 있게 변환하는 것이 특징 공간 변환이라고 한다.
이렇게 변환을 통해서 좋은 특징 공간을 자동으로 찾아내는 것을 표현 학습이라고 한다.
차원에 대한 몇 가지 설명
🔥 차원이 증가한다고 수식이나 알고리즘이 바뀌어야 하는 것은 아니다. 🔥
만약 3차원 특징 공간에 존재하는 두 점 a = (a₁, a₂, a₃)ᵀ, b = (b₁, b₂, b₃)ᵀ가 주어진다면 a와 b의 거리는 아래와 같다.
거리(a, b) = √(a₁ - b₁,)² + (a₂ - b₂)² + (a₃ - b₃) ²
이 방법은 d 차원으로 확장하면 아래의 식처럼 만들 수 있다.
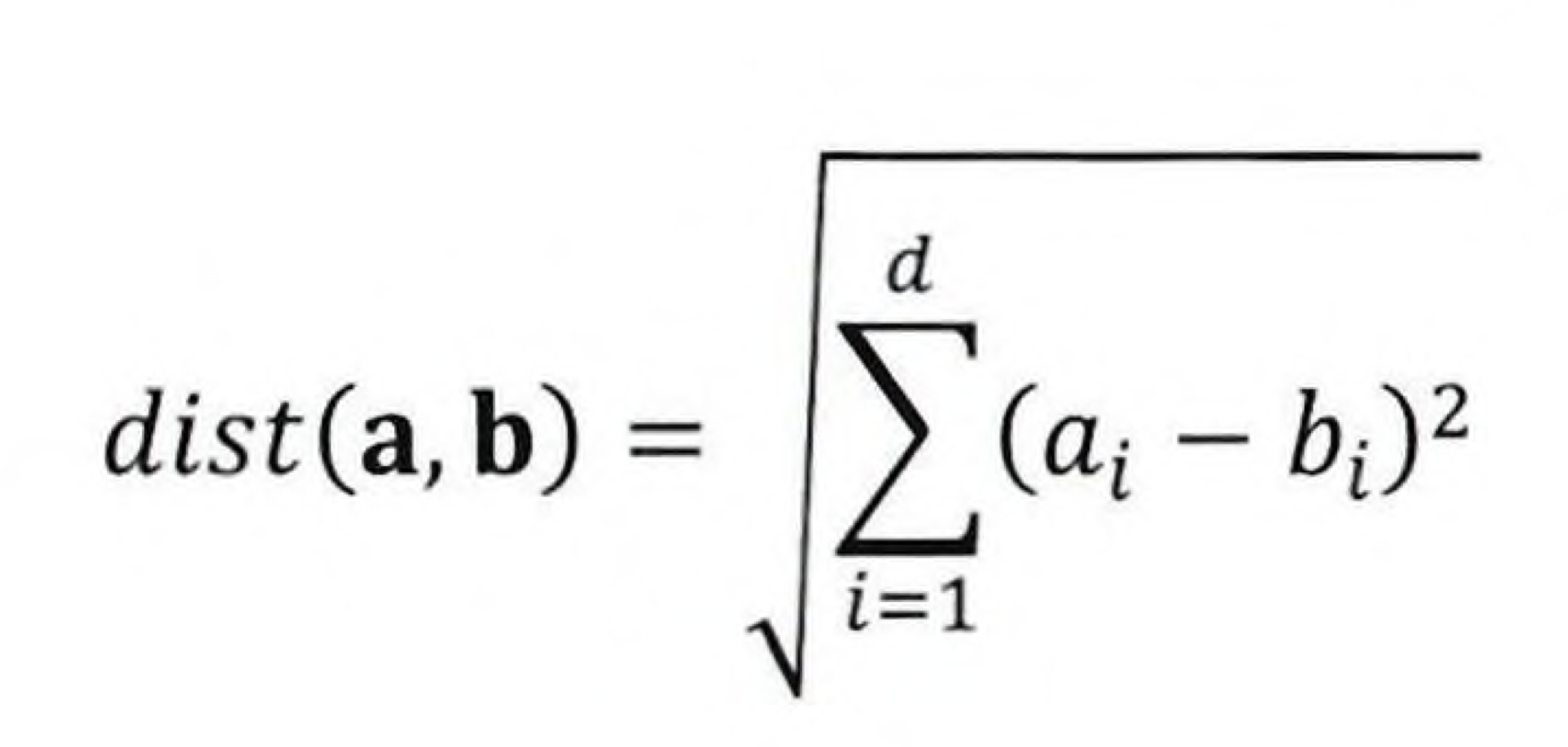
이 식을 통해서 고차원에서 계산을 하면 현실적인 문제가 발생한다. 차원이 높아지면서 거대한 특징 공간이 형성되고 데이터 포인트의 거리가 멀어진다. 따라서 모델의 성능이 저하된다.
'기계학습 - 오일석 > Chapter 1: 소개' 카테고리의 다른 글
| 1.7 기계 학습 유형 (0) | 2024.12.24 |
|---|---|
| 1.5 모델 선택 (0) | 2024.12.24 |
| 1.4 간단한 기계 학습의 예 (1) | 2024.12.24 |
| 1.1 기계 학습이란 (0) | 2024.12.23 |


