베이즈 정리를 통한 사전 확률(Prior)과 사후 확률(Posterior), 우도(Likelihood)

우선 베이즈 정리를 알기 전 결합 확률(joint prbability)와 조건부 확률(condition probability)에 대해서 알아야한다.
 

결합 확률 - P(x, y)

결합 확률이란 x사건과 y사건이 동시에 일어날 확률을 의미한다.
 
 

조건부 확률 - P(x | y)

조건부 확률이란 y사건이 일어난 후 x사건이 일어날 확률을 의미한다.
 
 

결합 확률과 조건부 확률의 관계 - P(x, y) = P(x| y)P(y)

결합 확률은 조건부 확률과 사건 x가 일어날 확률을 곱한 식으로 나타낼 수 있다. 
 
 

---

 

베이즈 정리

 
이러한 관계를 이용해서  베이즈 정리를 정의할 수 있다. 일반적으로 P(x, y)와 P(y, x)의 확률이 같기때문에 아래의 식이 성립된다.

 
 
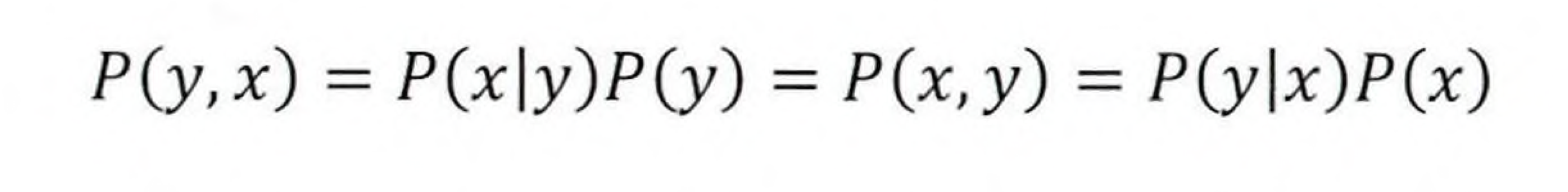
위 식을 P(y|x)에 대해서 정리를 하면 아래와 같이 베이즈 정리가 나온다. 
 

왼쪽) 베이즈 정리 / 오른쪽) 베이즈 정리가 모수 추정을 목적하다는 식

 
 
사건 A를 이 사람이 거짓말을 한 경우이고, 사건 B를 거짓말 탐지기가 거짓말이라고 판정한 경우라고 생각해서 위의 식을 해석해보겠다.
 

 
즉, 거짓말 탐지기가 거짓말이라고 판정했을 때 이 사람이 거짓말을 할 확률에 대한 식이다. 하지만 이렇게 매번 거짓말 탐지기 결과에 따라서 거짓말인지 아닌지를 계산하기는 어렵다. 따라서, 우리가 알 수 있는 정보들을 계산해서 원하는 확률을 구할 수 있다.
 
그래서 우도와 사전 확률을 곱한 값에 evidence(결과가 발생할 전체 확률)를 나눈 값을 통해서 사후 확률 값을 구할 수 있다. 
 
 

우도

우도라는 것은  B가 일어났을 때 A가 일어날 확률인 사전 확률을 반대로 A가 일어났을 때 B가 일어날 확률을 구하는 것이다. 즉, 사전 확률에서 결과(A)가 조건이 되어 그 조건을 수행했을 때 사전확률에서 조건(B)이 결과로 잘 나오는지를 확인하는 것이다. 
 
위의 식을 바탕으로 하면 거짓말 탐지기가 거짓말이라고 판정했을 때 이 사람이 거짓말을 할 확률에 대한 사전확률을 반대로 이 사람이 거짓말을 했을 때 거짓말 탐지기에서 거짓말이라고 나올 확률을 의미한다. 
 

사전 확률

사전 확률이라는 것은 새로운 관찰이 이루어지기 전에 미리 가지고 있는 기존 정보에 기반한 확률을 의미한다.
위의식을 바탕으로 하면 이 사람이 거짓말을 평소에 하는 확률을 의미한다. 
 

사후 확률 

사후 확률이라는 것은 새로운 관찰의 결과를 반영한 후 (B), 사건 A가 일어날 확률을 의미한다. 
즉, 거짓말 탐지기가 거짓말이라고 판정했을 때 이 사람이 거짓말을 할 확률을 의미한다.
 
 

질병을 예를 들어 사전 확률과 사후 확률 설명하기

예를 들어 A라는 병이 있고 어떤 환자가 이 병이 의심되어 병원에서 검사를 한다고 가정했을 떄, 병을 검사하기 전에 이 병이 얼마나 걸리기 어려운지, 쉬운지에 따라 병이 걸릴 확률을 확인하는 것을 "사전 확률"이라고 하고, 병을 검사하고 양성 결과를 반영해 실제로 병에 걸렸을 가능성을 "사후 확률"이라고 한다. 
 
 

---

 
 

모수 추정으로 표현한 사후 확률과 우도

0. θ와 x의 의미

θ는 확률 분포를 구성하는 Parameter를 의미(쉽게 말해서, 확률 분포를 결정하는 변수)하고, x는 관측값(데이터 또는 사건)을 의미한다.
 

---

1. 모수 추정에서의 우도, 사전 확률, 사후 확률의 의미

우도는 θ(매개변수)가 x(데이터)를 얼마나 잘 설명하는지를 평가하는 것이고, 사전 확률은 관찰하기 전 θ(매개변수)에 대해 가지고 있는 초기 지식을 의미하고, 사후 확률은 사전확률과 우도를 결합해서 데이터에 맞게 갱신된 θ(매개변수)에 대한 확률을 의미한다. 
 
 
 

---

 

2. 단일 데이터의 우도 

 
L(θ|x)는 관측값(x)이 주어질 때, 확률 분포(θ)가 얼마나 관측값(x)를 잘 설명하는지 보는 것이다. 쉽게 말해서, 데이터가 주어질 때 그 데이터의 실제 확률 분포와 비슷한 확률 분포가 나올 확률이다.
 
P(x|θ)는 확률 분포(θ)가 주어질 때, 관측값(x)이 나올 확률이다. 쉽게 말해서, 확률 분포가 고정된 상태에서, 그 분포에 따라 무작위로 얻어지는 다양한 데이터 값(관측값)들을 의미한다.
 
 

---

 

3. 독립 데이터의 우도

서로 독립적인 데이터 x1, x2, ... , xn이 주어졌다면,  데이터 집합의 실제 확률 분포와 비슷한 확률 분포가 나올 확률은 개별 데이터의 확률을 곱하는 방식으로 표현할 수 있다. 
 

---